Jeoistatistik, jeolojik verileri analiz etmek ve yorumlamak için kullanılan güçlü bir araçtır. Bu araçlardan biri olan Z testi, iki veri kümesi arasındaki ortalama farkın istatistiksel olarak anlamlı olup olmadığını belirlemek için kullanılır. Bu makalede, jeolojide Z testinin nasıl kullanıldığını detaylı ve kapsamlı bir şekilde inceleyeceğiz.
Z Testinin Temelleri
Bu Z testi, iki veri kümesi arasındaki ortalama farkın istatistiksel olarak anlamlı olup olmadığını belirlemek için kullanılan bir hipotez testidir. Bu test, normal dağılıma dayanan Z istatistiğini kullanır ve p-değeri aracılığıyla sonuçların yorumlanmasına imkan tanır.
Z İstatistiğinin Hesaplanması
Aşağıdaki formülle hesaplanır:
Z = (x̄₁ - x̄₂) / √(σ₁² / n₁ + σ₂² / n₂)
Formülde
- x̄₁: Birinci veri kümesinin ortalaması
- x̄₂: İkinci veri kümesinin ortalaması
- σ₁²: Birinci veri kümesinin varyansı
- σ₂²: İkinci veri kümesinin varyansı
- n₁: Birinci veri kümesinin örneklem büyüklüğü
- n₂: İkinci veri kümesinin örneklem büyüklüğü
Z İstatistiğinin Dağılımı
Z istatistiği, her iki veri kümesi de normal dağılıma sahipse ve örneklem büyüklükleri yeterince büyükse standart normal dağılıma (ortalama 0, standart sapma 1) uyar.
Merkezi Sınır Teoremi
Merkezi sınır teoremine göre, her iki veri kümesi de normal dağılıma sahipse ve örneklem büyüklükleri yeterince büyükse (genellikle n ≥ 30), Z istatistiği standart normal dağılıma (ortalama 0, standart sapma 1) uyar.
Standart Normal Dağılım
Standart normal dağılım, çan eğrisi olarak da bilinen simetrik bir dağılımdır. Bu dağılımda, Z istatistiğinin:
- %68’i -1 ve 1 arasında yer alır.
- %95’i -2 ve 2 arasında yer alır.
- %99.7’si -3 ve 3 arasında yer alır.
Z İstatistiğinin Dağılımını Etkileyen Faktörler
Z istatistiğinin dağılımını etkileyen iki temel faktör vardır:
- Veri kümelerinin normal dağılıma uyması: Veri kümeleri normal dağılıma uymuyorsa, Z istatistiği standart normal dağılımdan sapma gösterebilir.
- Örneklem büyüklükleri: Örneklem büyüklükleri yeterince büyük değilse, Z istatistiğinin dağılımı standart normal dağılımdan biraz farklı olabilir.
P-Değeri Hesaplanması
Z istatistiğinin standart normal dağılımında gözlemlenme olasılığını gösterir.
P-değeri, aşağıdaki formülle hesaplanır:
p-değer = P(Z < z) veya p-değer = P(Z > z)
Formülde
- Formüldeki z: Hesaplanan Z istatistiği değeri
- P(Z < z): Z istatistiğinin z’den küçük olma olasılığı
- P(Z > z): Z istatistiğinin z’den büyük olma olasılığı
Hipotez Testi
Hipotez testi, bir araştırma sorusuna veya hipoteze dayalı olarak veri kümelerini analiz etmek için kullanılan istatistiksel bir yöntemdir. Bu test, iki hipotez arasındaki farkı test ederek ve p-değeri gibi istatistiksel ölçütleri kullanarak hipotezlerin doğruluğunu değerlendirmeye yardımcı olur.
Z testi, genellikle aşağıdaki hipotezler ile kullanılır:
- H0 (Boş Hipotez): İki veri kümesinin ortalamaları arasında istatistiksel olarak anlamlı bir fark yoktur.
- H1 (Alternatif Hipotez): İki veri kümesinin ortalamaları arasında istatistiksel olarak anlamlı bir fark vardır.
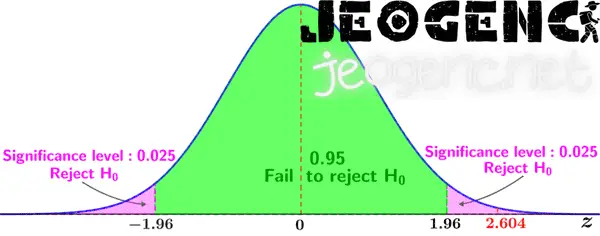
P-değeri 0.05’ten küçükse H0 reddedilir ve H1 kabul edilir. Bu, iki veri kümesinin ortalamaları arasındaki farkın istatistiksel olarak anlamlı olduğu anlamına gelir. P-değeri 0.05’ten büyükse H0 reddedilemez ve H1 hakkında kesin bir sonuca varılamaz.
Z Testinin Gücü
Z testi, iki veri kümesi arasındaki ortalama farkın istatistiksel olarak anlamlı olup olmadığını belirlemek için kullanılan bir hipotez testidir. İlgili Z testinin gücü, testin H1’i doğru şekilde reddetme olasılığını gösterir. Güçlü bir test, H1 doğruysa onu yüksek bir olasılıkla reddederken, zayıf bir test H1’i reddetmede daha az başarılı olabilir.
Z Testinin Gücünü Etkileyen Faktörler
Z testinin gücünü etkileyen iki temel faktör vardır:
Örneklem Büyüklüğü
Örneklem büyüklüğü arttıkça, Z testinin gücü de artar. Bunun nedeni, daha büyük örneklemden elde edilen verilerin daha güvenilir olması ve H1’i doğru şekilde reddetme olasılığını artırmasıdır.
Varyans
Veri kümelerinin varyansı arttıkça, Z testinin gücü azalır. Varyans, veri kümelerindeki değerlerin ortalamadan ne kadar sapma gösterdiğini ölçer. Varyans yüksek olduğunda, H1’i doğru şekilde reddetmek daha zor hale gelir.
Z Testinin Gücünü Hesaplama
Z testinin gücü, aşağıdaki formülle hesaplanabilir:
Güç = 1 - β = P(Z > zα)
Formülde
- β: Hata olasılığı (H1 doğruyken H0’i reddetme olasılığı)
- zα: 1 – α risk seviyesine karşılık gelen Z istatistiği değeri (α tip hata olasılığı)
- z: Hesaplanan Z istatistiği değeri
Z Testinin Sınırlamaları
Bu Z testinin bazı sınırlamaları da vardır. Bunlardan birkaçı:
- Verilerin normal dağılıma sahip olması gerekir.
- Örneklem büyüklükleri yeterince büyük olmalıdır.
- Veri kümelerinde aykırı değerler olmamalıdır.
Jeolojide Z Testi Uygulamaları
Z testi, jeolojide çeşitli alanlarda kullanılan güçlü bir istatistiksel araçtır. İki veri kümesi arasındaki ortalama farkın istatistiksel olarak anlamlı olup olmadığını belirlemek için kullanılır. Z testi, jeolojide aşağıdakiler gibi çeşitli alanlarda kullanılabilir:
Kayaç Türlerinin Sınıflandırılması
Kayaç türlerinin sınıflandırılması, jeolojinin temel bir bileşenidir. Jeologlar, kayaçları mineral bileşimi, dokusu ve kimyasal bileşimi gibi çeşitli özelliklere göre sınıflandırırlar. Z testi, kayaç türlerini sınıflandırmada kullanılan güçlü bir araçtır. Farklı kayaç türlerinin ortalama yoğunluklarını veya element konsantrasyonlarını karşılaştırmak için kullanılabilir.
Z Testinin Kayaç Türlerinin Sınıflandırılmasında Kullanımı
Z testi, kayaç türlerini sınıflandırmada aşağıdaki gibi kullanılabilir:
Ortalama Yoğunluk Karşılaştırması
Farklı kayaç türlerinin ortalama yoğunluklarının istatistiksel olarak farklı olup olmadığını belirlemek için Z testi kullanılabilir. Örneğin, bir jeolog, granit ve bazalt kayaç türlerinin ortalama yoğunluklarının istatistiksel olarak farklı olup olmadığını belirlemek için Z testi yapabilir.
Element Konsantrasyonu Karşılaştırması
Farklı kayaç türlerinin belirli elementlerin ortalama konsantrasyonlarının istatistiksel olarak farklı olup olmadığını belirlemek için Z testi kullanılabilir. Örneğin, bir jeolog, granit ve bazalt kayaç türlerinde ortalama silis konsantrasyonlarının istatistiksel olarak farklı olup olmadığını belirlemek için Z testi yapabilir.
Jeokimyasal Anomalilerin Belirlenmesi
Jeokimyasal anomaliler, bir bölgedeki element konsantrasyonlarının, bölgenin doğal arka plan değerlerinden anlamlı olarak farklı olduğu alanlardır. Bu anomaliler, mineral yatakları, çevre kirliliği veya jeolojik süreçler gibi çeşitli faktörlerden kaynaklanabilir. Jeokimyasal anomalileri belirlemek için çeşitli istatistiksel yöntemler kullanılabilir.
En yaygın yöntemlerden biri Z testidir. Z testi, bir elementin konsantrasyonunun ortalama arka plan değerinden kaç standart sapma uzaklıkta olduğunu hesaplar. Z değeri 2’den büyük veya -2’den küçük ise, element konsantrasyonunun arka plandan anlamlı olarak farklı olduğu kabul edilir.
Hidrojeolojik Parametrelerin Tahmini
Hidrojeolojik parametreler, yeraltı suyu akışı ve taşınımını tanımlayan ölçümlerdir. Bu parametreler, yeraltı suyu seviyeleri, akış hızı, hidrodinamik dispersivite ve porozite gibi değerleri içerir.
Hidrojeolojik parametrelerin tahmini, yeraltı suyu kaynaklarının yönetimi ve korunması için önemlidir. Bu parametreler, yeraltı suyu modellerini geliştirmek ve yeraltı suyunun gelecekteki davranışını tahmin etmek için kullanılır. Hidrojeolojik parametreleri tahmin etmek için çeşitli yöntemler kullanılabilir. Bu yöntemler şunlardır:
Doğrudan Ölçümler
- Yeraltı suyu seviyeleri: Piezometreler veya gözlem kuyuları kullanılarak ölçülür.
- Akış hızı: Tracer testleri veya Darcy kanunu kullanılarak tahmin edilir.
- Hidrodinamik dispersivite: Tracer testleri kullanılarak tahmin edilir.
- Porozite: Laboratuvar testleri veya jeofizik yöntemler kullanılarak tahmin edilir.
Dolaylı Yöntemler
- Jeofizik Yöntemler: Elektriksel resistivite, jeofizik tomografi ve sismik yöntemler gibi jeofizik yöntemler, yeraltı suyunun ve kayaların özelliklerini tahmin etmek için kullanılabilir.
- Sayısal Modelleme: Yeraltı suyu akışı ve taşınımını simüle etmek için sayısal modeller kullanılabilir. Bu modeller, hidrojeolojik parametreleri tahmin etmek için ters çözüm teknikleri ile kullanılabilir.
Jeoteknik Modelleme
Jeoteknik modelleme, mühendislik problemlerini çözmek için toprak ve kayaç davranışının simülasyonudur. Bu problemler, binaların ve altyapının tasarımı ve inşası, yamaç stabilitesi ve toprak kayması analizi, ve yeraltı suyu akışı ve kirliliği gibi alanları kapsar. Jeoteknik modellemede çeşitli yöntemler kullanılır. Bu yöntemler şunlardır:
Analitik Yöntemler
Bu yöntemler, basit problemleri çözmek için matematiksel denklemler kullanır.
Analitik yöntemler genellikle hızlı ve kolaydır, ancak karmaşık problemleri çözmek için uygun olmayabilir.
Sayısal Yöntemler
Bu yöntemler, problemleri çözmek için bilgisayarları kullanır.
Sayısal yöntemler karmaşık problemleri çözmek için daha uygundur ve analitik yöntemlerden daha doğru sonuçlar verebilir.
Fiziksel Modelleme
Bu yöntemde, problemin ölçekli bir modeli inşa edilir ve model üzerinde deneyler yapılır.
Fiziksel modelleme, karmaşık problemleri görselleştirmek ve anlamak için useful bir araç olabilir.
Jeoteknik modellemede Z testinin kullanımı
- Toprak veya kayaç mekanik parametrelerinin ortalama değerlerini tahmin etmek: Geçmişteki test sonuçları kullanılarak ortalama değer ve standart sapma hesaplanabilir. Yeni bir test sonucunun ortalamadan anlamlı olarak farklı olup olmadığını belirlemek için Z testi kullanılabilir.
- Bir bölgenin jeoteknik riskini değerlendirmek: Z testi, bir bölgenin deprem, heyelan veya yeraltı suyu akışı gibi jeoteknik risklere karşı ne kadar hassas olduğunu belirlemek için kullanılabilir.
