Ekstrapolasyon, bilinen bir değerler veya gerçekler dizisinin genişletilmesine dayalı olarak bilinmeyen bir değerin tahmin edilmesi anlamına gelir. Tahmin yapmak, mevcut bilgilerden açıkça belirtilmeyen bir şey çıkarmaktır. Enterpolasyon, bir değerler dizisi içinde var olan bilinen iki değer içindeki bir değeri tahmin etme eylemidir.
Ekstrapolasyonu ve Enterpolasyonu anlama
Hem ekstrapolasyon hem de enterpolasyon, diğer veri noktalarının gözlemine dayalı olarak bilinmeyen bir değişken için varsayımsal değerleri belirlemek veya tahmin etmek için faydalı yöntemlerdir. Ancak, bu yöntemleri birbirinden ayırt etmek ve birbirlerinden nasıl farklı olduklarını anlamak zor olabilir. Bu farklılıkları anlamanın en kolay yollarından biri, her terimin önekini anlamaktır. Extra- “ek olarak” anlamına gelirken enter- “arasında” anlamına gelir. Bu nedenle, ekstrapolasyon, bir kullanıcının mevcut değerlere ek olarak bir değer bulmaya çalıştığını gösterirken , enterpolasyon, mevcut değerler arasında yeni bir değer belirlemek istedikleri anlamına gelir.
| Enterpolasyon | ekstrapolasyon |
| Bir veri setinde iki nokta arasındaki değerlerin okunması | Veri kümesinin dışındaki bir değeri tahmin etme |
| Öncelikle eksik geçmiş değerleri belirlemek için kullanılır | Tahminde önemli bir rol oynar |
| Tahmini kaydın doğru olma olasılığı daha yüksektir. | Tahmini değerler yalnızca olasılıklardır, bu nedenle tamamen doğru olmayabilirler. |
Enterpolasyon bir örnekle açıklayalım
Enterpolasyon, belirli bir veri kümesindeki mevcut değerlerden bir değer belirlemek anlamına gelir. Bunu tanımlamanın başka bir yolu, diğer iki değer arasına bir ara değer ekleme veya araya sokma eylemidir. Veri biliminde veya matematikte enterpolasyon, belirli bir dizideki diğer veri noktalarının değerine dayalı olarak bir fonksiyonun değerini hesaplamakla ilgilidir. Bu fonksiyon f(x) olarak gösterilebilir ve bilinen x değerleri x 0 ile x n arasında değişebilir.
Örneğin, bir y = 3x + 4 regresyon çizgimiz olduğunu varsayalım. Bu “en uygun” çizgiyi üretmek için x’in değerinin 0 ile 10 arasında olması gerektiğini biliyoruz. Diyelim ki x = 6’yı seçtik. -Satır ve denklemi sığdırırsak, y’nin değerini aşağıdaki gibi tahmin edebiliriz:
y = 3(6) + 4 = 22
x değerimiz (6), en uygun çizgiyi yapmak için kullanılan kabul edilebilir x değerleri aralığındadır, bu nedenle bu, enterpolasyonla hesapladığımız geçerli bir y değeridir.
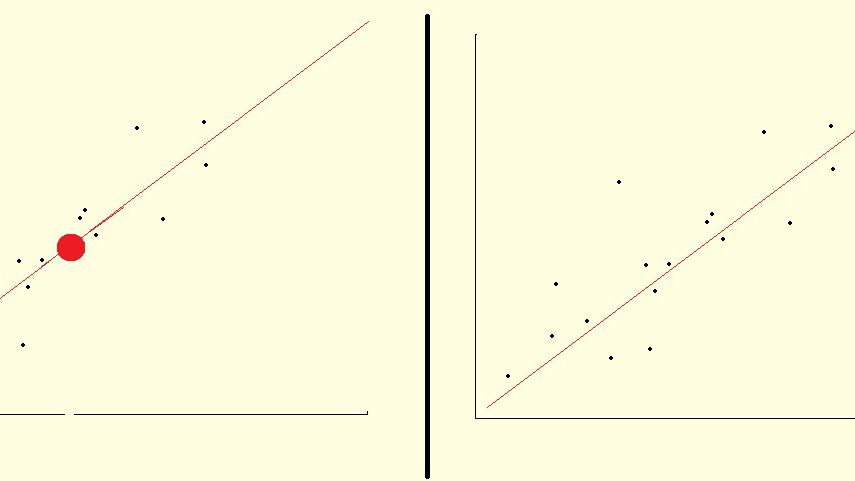
Ortak enterpolasyon yöntemleri
En yaygın enterpolasyon yöntemlerinden üçü şunlardır:
- doğrusal enterpolasyon
- polinom enterpolasyonu
- spline enterpolasyonu
Doğrusal enterpolasyon
Doğrusal enterpolasyon, en basit enterpolasyon yöntemlerinden biridir. Burada, diğer bilinmeyen değerleri belirlemek için bir grafik üzerinde iki nokta arasına düz bir çizgi çizilir. Basit yöntem sıklıkla yanlış tahminlerle sonuçlanır.
Polinom enterpolasyonu
Polinom enterpolasyonunda, bir veri setindeki eksik değerleri tahmin etmek için bir grafik üzerinde polinom fonksiyonları kullanılır. Daha kesin ve doğru bir yöntemdir. Polinomun grafiği, bu noktalar arasındaki verileri bulmak için bilinen noktalar arasındaki eğriyi doldurur.
Birden çok polinom enterpolasyonu yöntemi vardır:
- Lagrange enterpolasyonu
- Newton polinom enterpolasyonu
- spline enterpolasyonu
Newton yöntemi, Newton’un bölünmüş farkları enterpolasyon polinomu olarak da bilinir . Lagrange ve Newton enterpolasyon yöntemleri, en küçük polinom fonksiyonu, yani veri setindeki veri noktalarından geçen olası en düşük dereceli polinom ile sonuçlanır. Her iki yöntem de aynı sonucu verir ancak sonuca ulaşmak için farklı hesaplamalar kullanır.
Spline enterpolasyonu
Spline enterpolasyonunda, eksik değerleri tahmin etmek ve bir veri setindeki boşlukları doldurmak için parçalı fonksiyonlar kullanılır. Lagrange ve Newton yöntemlerinde olduğu gibi tüm veri seti için tek bir polinom tahmin etmek yerine, spline enterpolasyonu verinin alt kümeleri için birden çok daha basit polinom tanımlar. Bu nedenle genellikle daha doğru sonuçlar verir ve daha güvenilir bir yöntem olarak kabul edilir.
Ekstrapolasyon bir örnekle açıklayalım
Ekstrapolasyon, belirli bir veri kümesinin dışında kalan varsayımsal değerleri tahmin etmekle ilgilidir. Ekstrapolasyonun tahmine dayalı kalitesi, genellikle geçmiş değerleri tahmin etmekle ilgili olan enterpolasyonun aksine , yöntemin genellikle bilinmeyen gelecekteki değerleri tahmin etmek için kullanıldığı anlamına gelir . Örneğin, bir veri kümesinin verilen dört değerden oluştuğunu varsayalım: 1, 3, 5 ve 7. Bu değerler bir grafikte çizildiyse ve satırın aynı şekilde devam etmesi bekleniyorsa, beşinci değer 9 olarak tahmin edilebilir.
Bu yöntemde son değer kesin olarak bilinmemektedir. Bununla birlikte, eğrinin yörüngesi hakkında zaten bilinenlere ve bilinen değerler dizisinin doğasına dayanarak bir dereceye kadar kesin olarak tahmin etmek mümkündür.
Ortak ekstrapolasyon yöntemleri
En yaygın ekstrapolasyon yöntemlerinden üçü şunlardır:
- doğrusal ekstrapolasyon
- polinom ekstrapolasyonu
- konik ekstrapolasyon
Doğrusal enterpolasyona benzer şekilde, doğrusal ekstrapolasyon, bir veri kümesinin dışındaki değerleri tahmin etmek için doğrusal bir işlev kullanmayı ve düz bir çizgi çizmeyi içerir. Polinom ekstrapolasyonu yönteminde bir grafikteki değerler polinom şekilleri ve fonksiyonları ile belirlenir. Konik ekstrapolasyon, bilinen verilerle konik kesitler kullanılarak bilinmeyen değerlerin belirlenmesini içerir.
Ekstrapolasyon ve enterpolasyon uygulama
Enterpolasyon genellikle bilinmeyen bir değerin geçerli bir tahminini sağlar, bu nedenle ekstrapolasyondan daha güvenilir bir tahmin yöntemi olarak kabul edilir. Her iki yöntem de farklı amaçlar için yararlıdır. Enterpolasyon, bir proje veya kullanım senaryosu için kayıtları tamamlamak için eksik veya kayıp geçmiş kayıtları tahmin etmek için özellikle yararlıdır. Ekstrapolasyon, bir dizi bilinen veya geçmiş değere dayalı olarak bir olay veya oluşum hakkında tahminlerde bulunmak için kullanılır.
Gerçek dünyada, enterpolasyon ve ekstrapolasyon, aşağıdakiler de dahil olmak üzere birçok alanda uygulanmaktadır:
- gerçek dünya problemlerini çözmek için bilinmeyen değerleri belirlemek için fonksiyon değerleri türetmek için matematik;
- hava tahmini modelleri oluşturmak, yağışları tahmin etmek veya bilinmeyen kimyasal konsantrasyon değerlerini tahmin etmek için bilim; ve
- Nüfus artışı veya bir hastalığın yayılması gibi gelecekteki verileri tahmin etmek için istatistikler.
