Bu yazıda, ortalama, medyan (ortanca) ve mod gibi temel parametreleri inceleyeceğiz. Verilerinizin merkezini ve dağılımını anlamanıza yardımcı olacak bu parametreler, istatistiksel analizlerde ve veri görselleştirmelerinde oldukça önemlidir.
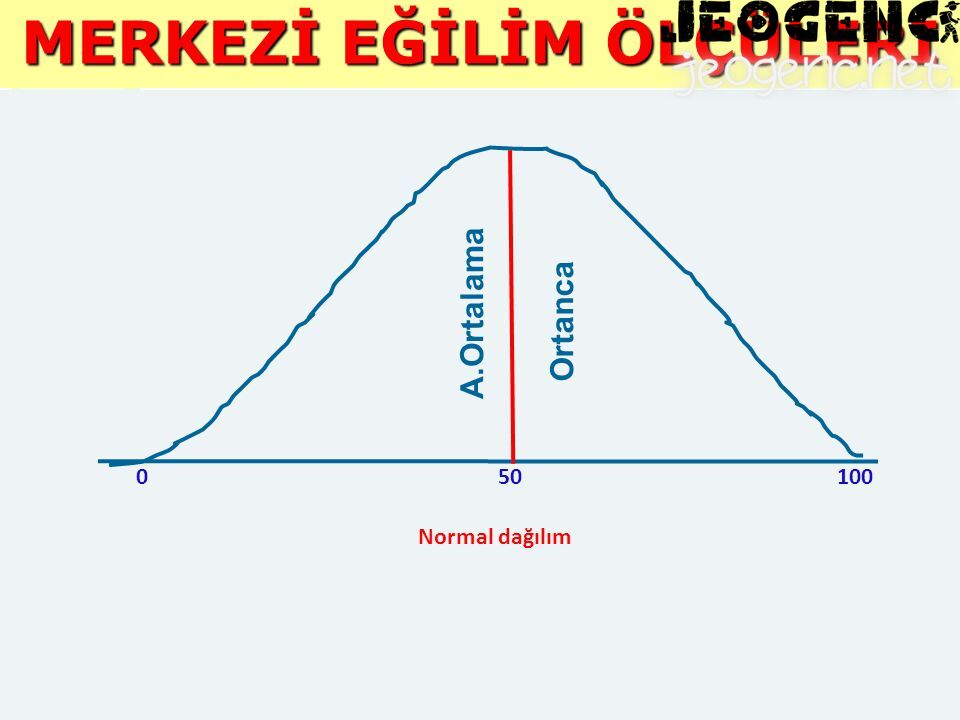
Tek bir populasyona ait simetrik bir çan eğrisini oluşturan frekans dağılımına ait başlıca merkezi eğilim parametreleri ortalama, medyan (ortanca) ve mod’dur. Aritmetik ortalama çan eğrisine ait simetri ekseninin, x-eksenini kestiği noktadır. İdeal bir normal dağılımda aritmetik ortalama, medyan (ortanca) ve mod üst üste çakışır.
Merkezi Eğilim Ne Demektir?
Merkezi eğilim, bir veri kümesinin ortalama değerini temsil eder. Farklı veri kümelerinin merkezini karşılaştırmak ve verilerin nasıl dağıldığını anlamak için kullanılır. Merkezi eğilimi hesaplamak için kullanılan çeşitli parametreler vardır, her birinin kendine özgü avantajları ve dezavantajları vardır.
Temel Merkezi Eğilim Parametreleri
Ortalama (Aritmetik Ortalama)
Ortalama, bir veri kümesindeki tüm değerlerin toplamının veri sayısına bölünmesiyle elde edilen sayısal bir ölçümdür. En yaygın kullanılan merkezi eğilim parametresidir ve veri kümesinin ortalama değerini temsil eder.
Hesaplama
Ortalama, aşağıdaki formülle hesaplanır:
Ortalama = Σxᵢ / n
Burada;
Σ (Sigma): Toplam işareti, veri kümesindeki tüm değerleri toplayacağımızı gösterir.
xᵢ: Veri kümesindeki her bir değeri temsil eder.
n: Veri kümesindeki toplam veri sayısıdır.
Örnek
Aşağıdaki tabloda 10 öğrencinin matematik sınavı notlarını görebilirsiniz:
| Öğrenci | Not |
|---|---|
| 1 | 75 |
| 2 | 82 |
| 3 | 68 |
| 4 | 95 |
| 5 | 87 |
| 6 | 71 |
| 7 | 65 |
| 8 | 98 |
| 9 | 73 |
| 10 | 81 |
Bu veri kümesinin ortalamasını hesaplamak için:
- Veri kümesindeki tüm notları toplayın: 75 + 82 + 68 + 95 + 87 + 71 + 65 + 98 + 73 + 81 = 805
- Toplam notu veri kümesindeki toplam öğrenci sayısına bölün: 805 / 10 = 80.5
Bu veri kümesinin ortalaması 80.5’tir.
Ortalama (Aritmetik Ortalama) Kullanım Alanları
Ortalama, birçok farklı alanda kullanışlı bir araçtır. Başlıca kullanım alanları şunlardır:
Normal Dağılım Gösteren Veri Kümelerinde
Normal dağılım gösteren veri kümelerinde, ortalama, veri kümesinin merkezini en iyi şekilde temsil eder. Bu tür veri kümelerinde, ortalama değer, veri kümesindeki değerlerin çoğunluğunun yakınında olacaktır.
Örnek:
Bir sınavda 100 öğrencinin aldığı notların ortalaması 75 ise, bu, öğrencilerin çoğunun 75 civarında not aldığı anlamına gelir.
Veri Kümelerinin Ortalama Değerlerini Karşılaştırmak İçin
Farklı veri kümelerinin ortalama değerlerini karşılaştırarak, veri kümeleri arasındaki farklılıkları ve benzerlikleri anlayabiliriz.
Örnek:
Bir şehrin farklı semtlerinde yapılan bir ankete göre, ortalama yaş 35 ise, bu şehirdeki diğer semtlerin ortalama yaşlarıyla karşılaştırılabilir.
Veri Kümelerinin Ortalama Eğilimlerini Anlamak İçin
Zaman içinde toplanan verilerin ortalamalarını inceleyerek, veri kümelerindeki eğilimleri ve değişimleri gözlemleyebiliriz.
Örnek:
Bir şirketin yıllık satışlarının ortalamalarını inceleyerek, şirketin satışlarının zaman içinde nasıl değiştiğini anlayabiliriz.
Ortalama Kullanmanın Avantajları
- Hesaplanması kolaydır.
- Veri kümesinin genel eğilimini temsil eder.
- Farklı veri kümelerini karşılaştırmak için kullanılabilir.
Ortalama Kullanmanın Dezavantajları
- Aşırı değerlere karşı hassasiyeti yüksektir. Aşırı değerler, ortalamayı veri kümesinin gerçek ortasından uzaklaştırabilir.
- Asimetrik veri kümelerinde tam olarak veri kümesinin merkezini yansıtmayabilir. Asimetrik veri kümelerinde, ortalama, veri kümesinin çoğunluğunun altında kalabilir.
Medyan (Ortanca)
Medyan, bir veri kümesindeki değerlerin küçükten büyüğe sıralanmasında tam ortasındaki değeri temsil eden sayısal bir ölçümdür. Ortalama gibi, medyan da bir veri kümesinin merkezi eğilimini gösterir. Fakat medyan, aşırı değerlerden etkilenmediği için asimetrik veri kümelerinde ve aşırı değerlerin var olduğu durumlarda ortalamadan daha uygun bir seçim olabilir.
Hesaplama
Medyan, aşağıdaki adımlarla hesaplanır:
- Veriler Küçükten Büyüğe Sıralanır: Veri kümesindeki tüm değerler, artan sırada sıralanır. Bu, veri kümesindeki değerlerin en küçükten en büyüğüne doğru sıralanması anlamına gelir.
- Veri Kümesinde Tek Sayıda Veri Varsa: Tam ortasındaki değer medyandır. Örneğin, 5 değeri olan bir veri kümesinde, tam ortasındaki 3. değer medyandır. Bu, veri kümesindeki değerlerin sıralanmış halinde 3. sırada yer alan değeri temsil eder.
- Veri Kümesinde Çift Sayıda Veri Varsa: Tam ortasındaki iki değerin ortalaması medyandır. Örneğin, 6 değeri olan bir veri kümesinde, tam ortasındaki 3. ve 4. değerlerin ortalaması medyandır. Bu, veri kümesindeki değerlerin sıralanmış halinde 3. ve 4. sırada yer alan değerlerin ortalamasını temsil eder.
Örnek
Aşağıdaki tabloda 10 öğrencinin matematik sınavı notlarını görebilirsiniz:
| Öğrenci | Not |
|---|---|
| 1 | 75 |
| 2 | 82 |
| 3 | 68 |
| 4 | 95 |
| 5 | 87 |
| 6 | 71 |
| 7 | 65 |
| 8 | 98 |
| 9 | 73 |
| 10 | 81 |
Bu veri kümesinin medyanını hesaplamak için:
- Verileri küçükten büyüğe sıralayın: 65, 68, 71, 73, 75, 81, 82, 87, 95, 98
- Veri kümesinde çift sayıda veri var (10 veri).
- Tam ortasındaki iki değerin ortalamasını hesaplayın: (75 + 81) / 2 = 78
Bu veri kümesinin medyanı 78’dir.
Matematiksel Olarak:
Medyanı hesaplamak için aşağıdaki formülü kullanabilirsiniz:
Medyan = (n + 1) / 2. sıradaki değer
Burada:
n: Veri kümesindeki veri sayısı
(n + 1) / 2: Tam ortasındaki değerin sıralaması
Kullanım Alanları
- Asimetrik veri kümelerinde
- Aşırı değerlerin var olduğu veri kümelerinde
- Nominal ve ordinal veri kümelerinde
Avantajları
- Aşırı değerlerden etkilenmez.
- Asimetrik veri kümelerinde veri kümesinin merkezini daha iyi temsil eder.
- Nominal ve ordinal veri kümelerinde kullanılabilir.
Dezavantajları
- Ortalama kadar bilgilendirici olmayabilir.
- Hesaplanması, ortalamaya göre biraz daha zordur.
Dikkat Edilmesi Gerekenler
- Medyan, her zaman veri kümesinin en bilgilendirici merkezi eğilim parametresi olmayabilir. Normal dağılım gösteren veri kümelerinde ortalama, medyandan daha uygun bir seçim olabilir.
- Medyan, sadece sayısal veriler için kullanılabilir. Nominal veya ordinal veriler için medyan hesaplanamaz.
Mod
Mod, bir veri kümesinde en sık görülen değeri temsil eden sayısal bir ölçümdür. Ortalama ve medyan gibi, mod da bir veri kümesinin merkezi eğilimini gösterir. Fakat mod, sayısal olmayan ve sınırlı sayıda değeri olan veri kümelerinde, yani nominal ve ordinal veri kümelerinde kullanışlı bir araçtır.
Hesaplama
Mod, bir veri kümesindeki her bir değerin frekansını sayarak ve en yüksek frekansa sahip değeri bularak hesaplanır. Frekans, bir değerin veri kümesinde kaç kez tekrarlandığını gösterir.
Mod Hesaplama Adımları:
- Verileri Listeleyin: Veri kümesindeki tüm değerleri bir liste halinde sıralayın.
- Değerleri Sayın: Her bir değerin veri kümesinde kaç kez tekrarlandığını sayın. Tekrarlanan her bir değer için bir frekans değeri hesaplayın.
- En Yüksek Frekansı Bulun: Frekans değerlerini karşılaştırın ve en yüksek frekansa sahip değeri belirleyin.
Örnek
Aşağıdaki tabloda 100 öğrencinin tercih ettiği renkleri görebilirsiniz:
| Renk | Frekans |
|---|---|
| Kırmızı | 25 |
| Mavi | 30 |
| Yeşil | 15 |
| Sarı | 20 |
| Turuncu | 10 |
Bu veri kümesinin modunu hesaplamak için:
- Her bir rengin frekansını sayın.
- En yüksek frekansa sahip rengi bulun.
- En yüksek frekansa sahip renk mavidir (30 kez tekrarlanmıştır).
Bu veri kümesinin modu mavidir.
Kullanım Alanları
- Nominal ve ordinal veri kümelerinde
- Veri kümelerinin en yaygın değerini anlamak için
- Anket sonuçlarını analiz etmek için
- Müşteri tercihlerini belirlemek için
Avantajları
- Nominal ve ordinal veri kümelerinde kullanılabilir.
- Hesaplanması kolaydır.
Dezavantajları
- Tek bir değere odaklandığı için veri kümesinin genel eğilimini tam olarak temsil etmeyebilir.
- Birden fazla mod değeri olabilir.
Dikkat Edilmesi Gerekenler
- Mod, her zaman veri kümesinin en bilgilendirici merkezi eğilim parametresi olmayabilir. Sayısal veri kümelerinde ortalama veya medyan daha uygun bir seçim olabilir.
- Mod, sadece sayısal olmayan ve sınırlı sayıda değeri olan veri kümelerinde kullanılabilir.
Hangi Parametreyi Kullanmalısınız?
Kullanmanız gereken parametre, veri kümenizin türüne ve analizinizin amacına bağlıdır.
- Normal dağılım gösteren veri kümeleri için: Ortalama, medyan ve mod genellikle birbirine yakın olacaktır.
- Asimetrik veri kümeleri için: Medyan, ortalamadan daha uygun bir seçim olabilir.
- Nominal veya ordinal veri kümeleri için: Mod, en bilgilendirici parametre olabilir.
Örnek Kullanım
Aşağıdaki tabloda, 10 öğrencinin matematik sınavı notlarını görebilirsiniz:
| Öğrenci | Not |
|---|---|
| 1 | 75 |
| 2 | 82 |
| 3 | 68 |
| 4 | 95 |
| 5 | 87 |
| 6 | 71 |
| 7 | 65 |
| 8 | 98 |
| 9 | 73 |
| 10 | 81 |
- Ortalama: (75 + 82 + 68 + 95 + 87 + 71 + 65 + 98 + 73 + 81) / 10 = 80.5
- Medyan: 75, 71, 73, 81, 82, 87, 95, 98. Medyan = 81
- Mod: 71, 73, 75, 81, 82, 87, 95, 98. Mod = 81
Bu örnekte, ortalama ve medyan birbirine yakındır. Bu da veri kümesinin normal dağılıma yakın olduğunu gösterir. Mod değeri ise 81’dir ve bu da 81 notunun veri kümesinde en sık görülen not olduğunu gösterir.
Merkezi eğilim parametreleri, verilerinizin kalbini anlamanıza ve veri kümelerini karşılaştırmanıza yardımcı olan temel istatistiksel araçlardır. Hangi parametreyi kullanmanız gerektiği, veri kümenizin türüne ve analizinizin amacına bağlıdır.
Bu yazıda, merkezi eğilim parametreleri hakkında temel bilgiler verdik. Daha fazla bilgi için istatistik kitaplarına veya internetteki kaynaklara başvurabilirsiniz.
