Jeoistatistikte korelasyon analizi, jeolojik veri setleri arasındaki ilişkiyi ve bağımlılığı ölçmek için kullanılan önemli bir istatistiksel araçtır. Bu analiz, jeolojik modelleme, haritalama ve risk değerlendirmesi gibi çeşitli alanlarda kritik bir rol oynar.

Korelasyon Nedir?

Korelasyon, iki değişken arasındaki ilişkinin gücünü ve yönünü ölçen bir istatistiksel değerdir. Bu değer, -1 ile +1 arasında değişir.

Korelasyon Katsayısı

Korelasyon katsayısı, Pearson korelasyon katsayısı (r) olarak da bilinir ve aşağıdaki formülle hesaplanır:

r = Σ[(x_i – x̄)(y_i – ȳ)] / √Σ[(x_i – x̄)^2 Σ[(y_i – ȳ)^2]

x_i ve y_i: Değişkenlerin i. veri noktası

x̄ ve ȳ: Değişkenlerin ortalamaları

Korelasyon Katsayısı Yorumlanması

Korelasyon katsayısı, iki değişken arasındaki ilişkinin gücünü ve yönünü gösteren bir sayıdır. Bu sayı -1 ile +1 arasında değişir.

Korelasyon Katsayısının Değerleri

+1: Mükemmel Pozitif Korelasyon: Bir değişkenden birinin artması diğerinin de artmasına neden olur. Örneğin, bir öğrencinin çalışma süresi arttıkça sınav notu da artar.
-1: Mükemmel Negatif Korelasyon: Bir değişkenden birinin artması diğerinin azalmasına neden olur. Örneğin, bir ürünün fiyatı arttıkça satışları da azalır.
0: Korelasyon Yok: İki değişken arasında hiçbir ilişki yoktur. Örneğin, bir kişinin boyu ile göz rengi arasında bir korelasyon yoktur.

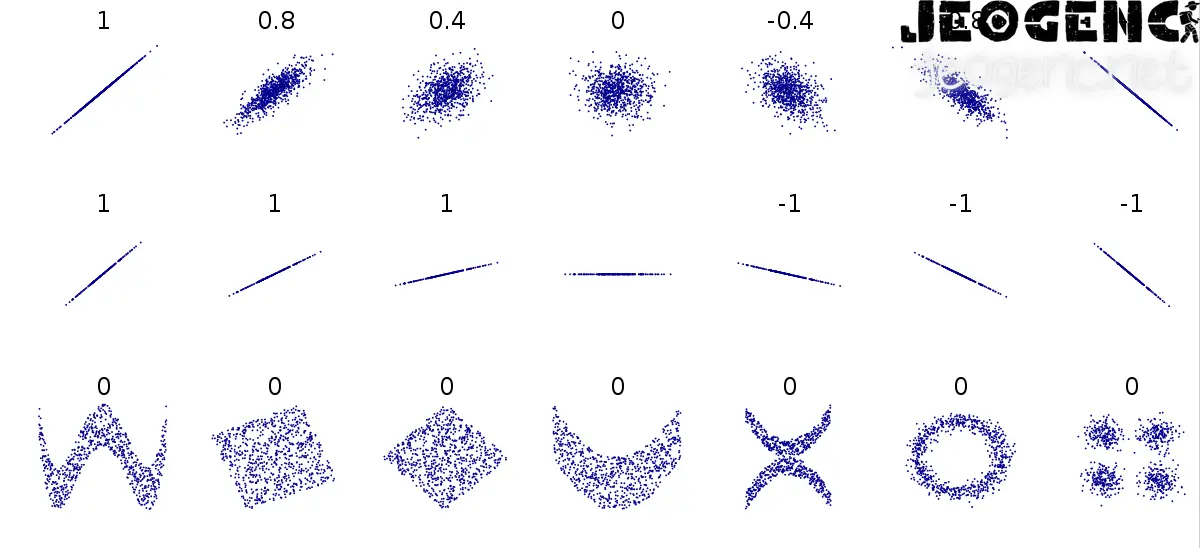
Korelasyon Katsayısının Yorumlanmasında Dikkat Edilmesi Gereken Noktalar

Korelasyonun katsayısı nedensellik göstermez. Bir değişkenden birinin diğerini etkilediğini varsaymak hatalı olabilir. Örneğin, dondurma satışlarının artması ile boğulma vakalarının da artması arasında bir korelasyon olabilir, ancak bu dondurmanın boğulmaya neden olduğu anlamına gelmez.

Korelasyon katsayısı yalnızca doğrusal ilişkileri ölçer. Doğrusal olmayan ilişkiler için Spearman korelasyon katsayısı kullanılmalıdır.
Korelasyon katsayısı veri setinin dağılımına duyarlıdır. Veriler normal dağılımdan saparsa, korelasyon katsayısı yanıltıcı olabilir.

Korelasyon Katsayısının Gücünü Değerlendirme

Korelasyon katsayısının mutlak değeri bize ilişkinin gücü hakkında bilgi verir.

0.2’den küçük: Zayıf ilişki
0.2 – 0.5 arasında: Orta derecede ilişki

0.5’ten büyük: Güçlü ilişki

Örnekler

Bir öğrencinin çalışma süresi ile sınav notu arasındaki korelasyon +0.8 ise, bu iki değişken arasında güçlü bir pozitif ilişki olduğunu gösterir.

Ürünün fiyatı ile satışları arasındaki korelasyon -0.6 ise, bu iki değişken arasında güçlü bir negatif ilişki olduğunu gösterir.
Bir kişinin boyu ile göz rengi arasındaki korelasyon 0.1 ise, bu iki değişken arasında zayıf bir ilişki olduğunu gösterir.

Jeoistatistikte Korelasyon Analizi Türleri

Jeoistatistikte, iki ana tür korelasyon analizi kullanılır:

Pearson Korelasyon Katsayısı

Tanımı: İki sayısal değişken arasındaki doğrusal ilişkinin gücünü ve yönünü ölçer.

Formülü

r = Σ[(x_i – x̄)(y_i – ȳ)] / √Σ[(x_i – x̄)^2 Σ[(y_i – ȳ)^2]

x_i ve y_i: Değişkenlerin i. veri noktası

x̄ ve ȳ: Değişkenlerin ortalamaları

Değerleri: -1 ile +1 arasında değişir.

Yorumu

+1: Mükemmel pozitif korelasyon (bir değişken artarken diğeri de artar)

-1: Mükemmel negatif korelasyon (bir değişken artarken diğeri de azalır)
0: Korelasyon yok (iki değişken arasında ilişki yok)

Sınırlamaları

Nedensellik göstermez.
Doğrusal olmayan ilişkileri ölçmez.
Veri dağılımına duyarlıdır.

Spearman Korelasyon Katsayısı

Tanımı: İki ordinal değişken (sıralama bazlı) veya sayısal değişkenler arasındaki doğrusal olmayan ilişkinin gücünü ve yönünü ölçer.

Formülü

r_s = 1 – 6Σd_i^2 / n(n^2 – 1)

d_i: İki değişkenin i. veri noktası sıralamaları arasındaki fark

n: Veri seti büyüklüğü

Değerleri: -1 ile +1 arasında değişir.

Yorumu

Pearson korelasyon katsayısına benzer.

Sınırlamaları

Pearson korelasyon katsayısına benzer.

Korelasyon Analizi Uygulamaları

Jeolojik Modelleme

Jeolojik modelleme, yeraltının üç boyutlu yapısını ve özelliklerini anlamak için kullanılan bir yöntemdir. Bu modeller, jeolojik haritalar, sondaj verileri, jeofizik veriler ve jeokimyasal veriler gibi çeşitli veri kaynaklarını kullanarak oluşturulur. Jeolojik modeller, çeşitli amaçlar için kullanılabilir:

Yeraltı kaynaklarının keşfi ve değerlendirilmesi: Petrol, doğalgaz, mineraller ve yeraltı suyu gibi kaynakların keşfedilmesi ve değerlendirilmesi için jeolojik modeller kullanılır.

Doğal afetlerin riskinin değerlendirilmesi: Deprem, heyelan ve sel gibi doğal afetlerin riskinin değerlendirilmesi için jeolojik modeller kullanılır.
Mühendislik projelerinin tasarımı: Tünel, baraj ve yol gibi mühendislik projelerinin tasarımı için jeolojik modeller kullanılır.
Çevresel etkilerin değerlendirilmesi: Kirlilik ve arazi kullanımı değişiklikleri gibi çevresel etkilerin değerlendirilmesi için jeolojik modeller kullanılır.

Jeolojik Modelleme Türleri

Statik modeller: Zamanla değişmeyen jeolojik özellikleri temsil eden modellerdir.
Dinamik modeller: Zamanla değişen jeolojik özellikleri temsil eden modellerdir.

Jeolojik Modellemede Kullanılan Yöntemler

Jeolojik haritalama: Jeolojik haritalar, yeraltındaki kayaç türlerinin ve yapıların dağılımını gösterir.
Sondaj: Sondaj, yeraltından kayaç ve toprak örnekleri toplamak için kullanılır.

Jeofizik: Jeofizik yöntemler, yeraltının fiziksel özelliklerini (örneğin, yoğunluk, elektriksel iletkenlik) ölçmek için kullanılır.
Jeokimya: Jeokimyasal yöntemler, yeraltındaki kayaç ve toprakların kimyasal bileşimini analiz etmek için kullanılır.

Jeolojik Modellemede Korelasyon Analizinin Kullanımı

Korelasyon analizi, farklı jeolojik katmanlar veya kayaç türleri arasındaki ilişkiyi modellemek için kullanılabilir. Örneğin:

Bir bölgedeki tortul kayaçların yaşı ile granit kayaçların yaşı arasındaki ilişkiyi modellemek için kullanılabilir.
Bölgedeki kayaç türü ile toprak tipi arasındaki ilişkiyi modellemek için kullanılabilir.

Bir bölgedeki jeolojik faylar ile deprem riski arasındaki ilişkiyi modellemek için kullanılabilir.

Haritalama

Haritalama, bir bölgenin jeolojik özelliklerinin dağılımını gösteren bir harita oluşturma işlemidir. Bu haritalar, jeolojik araştırmalar, mühendislik projeleri ve çevresel değerlendirmeler gibi çeşitli amaçlar için kullanılır.

Haritalama Türleri

Jeolojik haritalar: Bir bölgenin kayaç türlerini, jeolojik yapılarını ve jeolojik geçmişini gösteren haritalardır.
Jeofizik haritalar: Bir bölgenin yeraltı fiziksel özelliklerini (örneğin, yoğunluk, elektriksel iletkenlik) gösteren haritalardır.

Jeokimyasal haritalar: Bir bölgenin yeraltındaki kayaç ve toprakların kimyasal bileşimini gösteren haritalardır.
Tehlike haritaları: Deprem, heyelan ve sel gibi jeolojik tehlikelerin riskini gösteren haritalardır.

Haritalamada Kullanılan Yöntemler

Jeolojik arazi çalışmaları: Jeologlar, jeolojik haritalar oluşturmak için arazide kayaç türlerini ve jeolojik yapıları gözlemler ve haritalar.
Uzaktan algılama: Uydular ve havadan fotoğraflar, jeolojik haritalar oluşturmak için kullanılır.
Jeofizik yöntemler: Jeofizik yöntemler, yeraltının fiziksel özelliklerini ölçmek için kullanılır ve bu bilgiler jeolojik haritalar oluşturmak için kullanılır.

Jeokimyasal yöntemler: Jeokimyasal yöntemler, yeraltındaki kayaç ve toprakların kimyasal bileşimini analiz etmek için kullanılır ve bu bilgiler jeolojik haritalar oluşturmak için kullanılır.

Korelasyon Analizinin Haritalamada Kullanımı

Korelasyon analizi, bir bölgenin jeolojik özelliklerinin dağılımını haritalamak için kullanılabilir. Örneğin:

Bir bölgedeki toprak mineral içeriği haritasını oluşturmak için kullanılabilir.
Bölgedeki yeraltı su seviyesi haritasını oluşturmak için kullanılabilir.
Bir bölgedeki jeolojik tehlikelerin (deprem, heyelan vb.) risk haritasını oluşturmak için kullanılabilir.

Risk Değerlendirmesi

Risklerin değerlendirmesi, doğal afetler veya jeolojik tehlikeler gibi potansiyel tehlikelerin neden olabileceği zararları tahmin etme ve bu zararları azaltmak için önlemler geliştirme sürecidir. Riskin değerlendirmesi, çeşitli alanlarda kullanılır:

Afet yönetimi: Doğal afetlerin neden olabileceği zararları tahmin etmek ve bu zararları azaltmak için planlar geliştirmek için kullanılır.

Mühendislik: Mühendislik projelerinin tasarımı sırasında potansiyel riskleri değerlendirmek ve bu riskleri azaltmak için önlemler geliştirmek için kullanılır.
Çevresel değerlendirme: Çevresel projelerin potansiyel risklerini değerlendirmek ve bu riskleri azaltmak için önlemler geliştirmek için kullanılır.

Risk Değerlendirmesi Aşamaları

Tehlike tanımlama: Potansiyel tehlikeleri ve bunların olasılıklarını belirlemek.
Hassasiyet analizi: Potansiyel tehlikelerden etkilenebilecek unsurları ve bunların ne kadar etkilenebileceğini belirlemek.
Risk analizi: Tehlike ve hassasiyet analizlerinin sonuçlarını birleştirerek riski hesaplamak.

Risk yönetimi: Riski azaltmak için önlemler geliştirmek ve uygulamak.

Korelasyon Analizinin Risk Değerlendirmesinde Kullanımı

Korelasyon analizi, doğal afetlerin veya jeolojik tehlikelerin riskini değerlendirmek için kullanılabilir. Örneğin:

Bir bölgedeki deprem riskini değerlendirmek için deprem büyüklüğü ile hasar arasındaki ilişkiyi inceleyebilir.
Bölgedeki heyelan riskini değerlendirmek için yağış miktarı ile heyelan sıklığı arasındaki ilişkiyi inceleyebilir.
Bir bölgedeki sel riskini değerlendirmek için nehir akış hızı ile taşkın riski arasındaki ilişkiyi inceleyebilir.

Korelasyon Analizinin Sınırlamaları

Korelasyon analizi, jeolojik veri setlerini analiz etmek için güçlü bir araç olsa da, bazı sınırlamaları da vardır. Bu sınırlamaların bilincinde olmak ve yorumları dikkatli yapmak önemlidir.

Nedensellik Göstermez

Korelasyon, iki değişken arasındaki ilişkinin gücünü ve yönünü gösteren bir istatistiksel ölçüttür. Ancak, korelasyon nedensellik göstermez. Bir değişkenden birinin diğerini etkilediğini varsaymak hatalı olabilir.

Örnek

Dondurma satışlarının artması ile boğulma vakalarının da artması arasında bir korelasyon olabilir. Bu, dondurma satışlarının arttıkça boğulma vakalarının da arttığı anlamına gelir. Ancak, bu dondurmanın boğulmaya neden olduğu anlamına gelmez. Bu korelasyonun başka nedenleri de olabilir:

Sıcak havalarda hem dondurma satışları hem de boğulma vakaları artabilir.
Dondurma yiyen insanlar daha fazla suya gidebilir ve bu da boğulma riskini artırabilir.
Boğulma vakaları artan yaz tatilleri ile ilişkili olabilir.

Nedensellik Göstermek için Neler Gereklidir

Zamansal Öncelik: Neden olarak kabul edilen değişken, sonuç olarak kabul edilen değişkenden önce gelmelidir.
Eşlik: Neden olarak kabul edilen değişkente bir değişim olduğunda, sonuç olarak kabul edilen değişkende de bir değişim olması gerekir.

Yalnızca Nedensellik: Neden olarak kabul edilen değişken dışında, sonuç olarak kabul edilen değişkeni etkileyen başka bir değişken olmamalıdır.

Nedensellik Göstermek için Kullanılan Yöntemler

Deneyler: Bir değişkende yapılan değişikliğin diğer değişken üzerindeki etkisini kontrol etmek için deneyler kullanılabilir.

Gözlemsel çalışmalar: Deney yapmak mümkün olmadığında, gözlemsel çalışmalar kullanılabilir. Bu çalışmalarda, iki değişken arasındaki ilişkiyi gözlemlemek için veriler toplanır.

Doğrusal Olmayan İlişkiler

Pearson korelasyon katsayısı, iki değişken arasındaki doğrusal ilişkinin gücünü ve yönünü ölçen bir istatistiksel ölçüttür. Ancak, doğrusal olmayan ilişkileri göz ardı eder. Bu, iki değişken arasındaki ilişki doğrusal değilse, Pearson korelasyon katsayısının yanıltıcı olabileceği anlamına gelir.

Doğrusal Olmayan İlişki Nedir?

Doğrusal olmayan bir ilişkide, iki değişken arasındaki ilişki bir doğru çizgi ile temsil edilemez. İlişki parabolik, üssel veya logaritmik olabilir.

Pearson Korelasyon Katsayısının Doğrusal Olmayan İlişkilerde Yanıltıcı Olmasının Nedenleri

Pearson korelasyon katsayısı, iki değişken arasındaki ortalama farkı hesaplar. Doğrusal olmayan bir ilişkide, ortalama fark yanıltıcı olabilir.
Korelasyon katsayısı, iki değişken arasındaki veri noktalarının dağılımını göz önünde bulundurmaz. Doğrusal olmayan bir ilişkide, veri noktaları bir doğrusal dağılımda olmayabilir.

Doğrusal Olmayan İlişkileri Ölçmek için Kullanılan Yöntemler

Spearman korelasyon katsayısı: İki değişken arasındaki sıra korelasyonunu ölçer.
Kendall tau korelasyon katsayısı: İki değişken arasındaki konkordans ve diskordans sayılarını kullanarak korelasyonu ölçer.
Regresyon analizi: Doğrusal olmayan ilişkileri modellemek için kullanılabilir.

Veri Dağılımına Duyarlıdır

Korelasyon katsayısı, iki değişken arasındaki ilişkinin gücünü ve yönünü gösteren bir istatistiksel ölçüttür. Ancak, veri setinin dağılımına duyarlıdır. Bu, veriler normal dağılımdan saparsa, korelasyon katsayısının yanıltıcı olabileceği anlamına gelir.

Normal Dağılım Nedir?

Normal dağılımda, veri noktaları ortalama değer etrafında simetrik bir şekilde dağılır. Verilerin çoğu ortalamaya yakın değerlere sahipken, daha az sayıda veri noktası ortalamadan uzaklaşır.

Korelasyon Katsayısının Veri Dağılımına Duyarlı Olmasının Nedenleri

Pearson korelasyon katsayısı, iki değişken arasındaki ortalama farkı hesaplar. Veriler normal dağılımdan saparsa, ortalama fark yanıltıcı olabilir.

Pearson korelasyon katsayısı, iki değişken arasındaki veri noktalarının dağılımını göz önünde bulundurmaz. Veriler normal dağılımdan saparsa, veri noktaları bir doğrusal dağılımda olmayabilir.

Korelasyon Katsayısını Yorumlarken Dikkat Edilmesi Gerekenler

Verilerin normal dağılımdan sapıp sapmadığını kontrol etmek.
Verilerin dağılımını görselleştirmek için histogram veya yoğunluk grafiği kullanmak.
Gerekirse Spearman korelasyon katsayısı veya Kendall tau korelasyon katsayısı gibi doğrusal olmayan korelasyon katsayıları kullanmak.

Ek Sınırlamalar

Korelasyon katsayısı aykırı değerlere duyarlıdır.
Korelasyon katsayısı değişkenlerin birimlerinden etkilenir.