Jeoloji mühendisliği ders programında yer alan jeoistatistik, jeolojik verilerin analizinde ve yorumlanmasında önemli bir rol oynar. Jeoistatistiksel analizler, örnekleme, veri görselleştirme, istatistiksel modelleme ve jeoistatistiksel kriging gibi çeşitli teknikleri kullanır. Bu teknikler, jeolojik veri setlerinden anlamlı bilgiler çıkarmaya ve jeolojik modeller oluşturmaya yardımcı olur.
Çok sayıdaki verilerin bir rapor, makale veya benzeri çalışalarda gösterilmesi veya bunlardan bir bakışta sonuç çıkarılabilmesi için belirli şekillerde düzenlenmesi gerekir. Bu amaç için kullanılan başlıca grafiksel düzenleme ve sunum yöntemleri bulunmaktadır. Veri görselleştirme, jeoistatistikte önemli bir adımdır. Karmaşık veri setlerini basit ve anlaşılır bir şekilde sunmak için çeşitli grafik türleri kullanılır. Bu makalede, jeoistatistikte sıklıkla kullanılan üç önemli grafik türüne odaklanacağız. Bunlar;
- Histogram ve frekans eğrileri,
- Dairesel grafikler ve
- Kutu grafikler
Histogram ve Frekans Eğrileri
Histogram, bir veri setindeki değerlerin dağılımını gösteren bir grafiktir. Dikey eksende frekans (veri noktalarının sayısı) ve yatay eksende veri değerleri yer alır. Frekans eğrisi ise, histogramların pürüzsüzleştirilmiş bir versiyonudur ve veri setinin olasılık yoğunluk fonksiyonunu gösterir.
Her istatiksel değerlendirmede bütün ölçüm ve gözlem sonuçları frekans dağılımları şeklinde düzenlenir. Frekans dağılımı, belirli gözlem sonucunun kütükte kaç defa bulunduğunu veya sınıf veya fraksiyon da denilen, bir aralıkta kaç ölçüm sonucunun yer aldığını gösterir. Doğal olaylara ait frekans olan, nispeten basit, matematiksel fonksiyonlara az veya çok uyarlar.
Burada özellikle, olasılık teorisinde olduğu gibi, istatistik uygulamalarında önemli bir rolü olan normal dağılımı belirlemek gerekir. Bunun dışında, alternatif imkanların ortaya çıkışlarını istatistiksel olarak tanımlayan binom dağılımını ve ender rastlanan istatistiksel değerlendirmelerde önem taşıyan poisson dağılımını da belirtmek gerekir.
Frekans dağılımı, bir özelliğin değişkenliğini tam olarak yansıtır, kayıt çizelgesindeki sayısal materyalin grafiklerle kolay anlaşılabilir şekilde ifade edilmesinde kullanılır ve çok önemli istatistiksel kavramlardan birini teşkil eder. Bu grafiklerden yararlanarak ortalama değer, varyans, ortanca ve mod kolaylıkla hesaplanır.
Histogram ve frekans eğrilerinin kullanım alanları
1. Veri setinin simetri ve eğrilik gibi özelliklerini değerlendirmek
Histogramın şekli, veri setinin simetri ve eğrilik hakkında bilgi verir. Simetrik bir histogram, verilerin ortalama değere yakın bir şekilde dağıldığını gösterir. Eğri bir histogram ise, verilerin ortalama değere göre eğilimli olduğunu gösterir.
2. Farklı veri setlerini karşılaştırmak
Farklı veri setlerinin histogram ve frekans eğrileri karşılaştırılarak, veri setlerinin dağılımları ve değişkenlikleri karşılaştırılabilir.
3. Anomaliler ve aşırı değerler tespit etmek
Histogram ve frekans eğrilerindeki ani değişimler, veri setinde anomali veya aşırı değerlerin varlığını gösterebilir.
4. İstatistiksel modelleme için veri setinin uygunluğunu değerlendirmek
Histogram ve frekans eğrileri, istatistiksel modelleme için veri setinin uygunluğunu değerlendirmek için kullanılabilir. Örneğin, normal dağılıma uymayan bir veri seti, bazı istatistiksel modeller için uygun olmayabilir.
Histogram ve frekans eğrilerinin yorumu
Histogram ve frekans eğrileri örnek miktarı ve örneğin özelliğine göre aşağıdaki görselde görüldüğü gibi farklı şekiller gösterir.
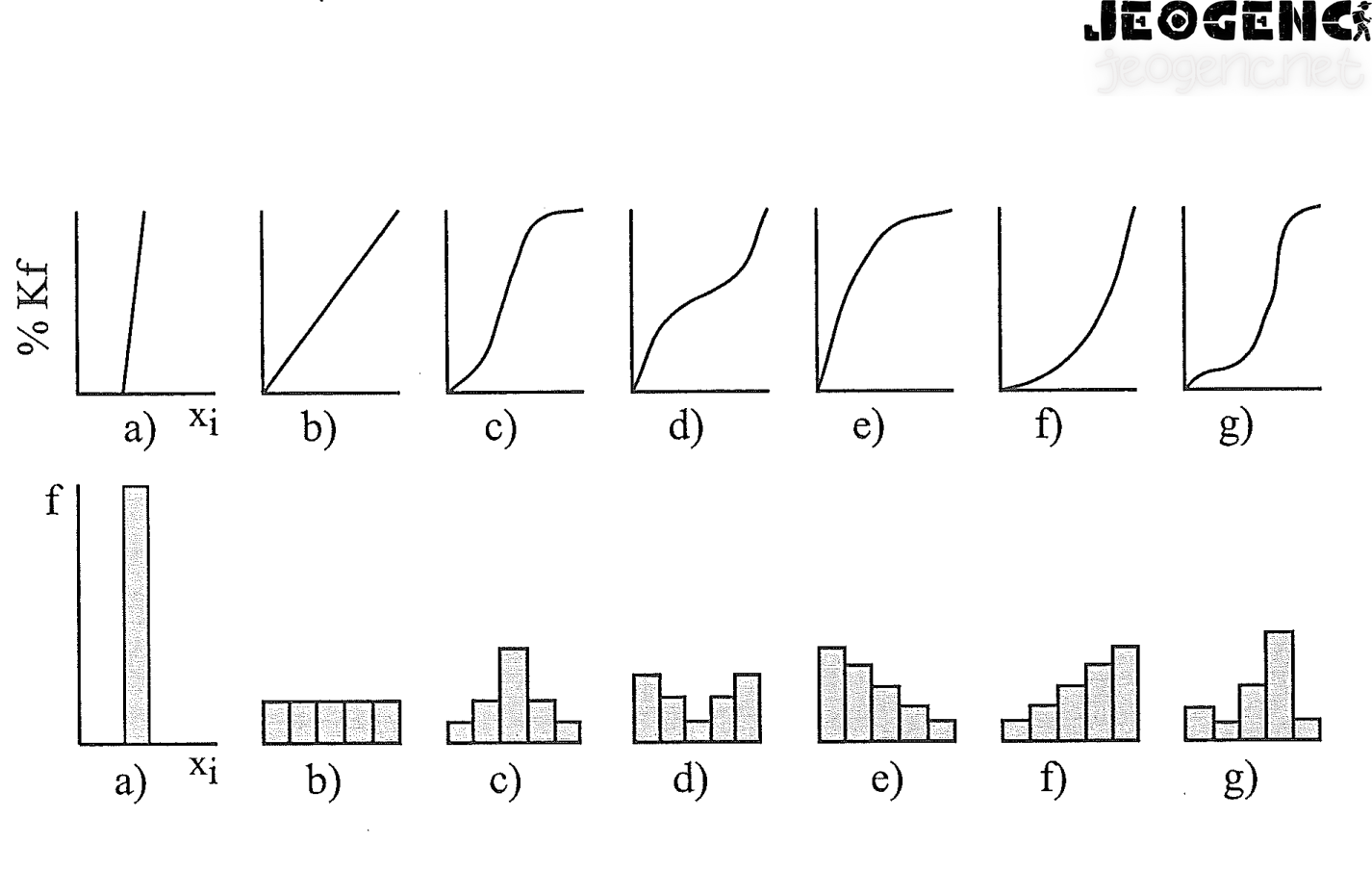
Bu şekillere göre örneklerin gösterdiği dağılımlar belirlenir ve dağılımın özelliği hakkında yorum yapılır. Dağılım simetrik bir durum arz ediyorsa, örneğin aritmetik ortalaması, standart sapması gibi parametrelerden yararlanarak ana kitle hakkında fikir yürütülebilir. Dağılım sağa veya sola çarpık yani asimetrik bir durum gösteriyorsa, örneğe ait parametreler, dağılım çeşitli dönüştürmeler ile simetrik duruma dönüştürüldükten sonra belirlenebilir.
Zira sağa çarpık durumda gerçek aritmetik ortalama değeri olduğundan fazla, buna karşılık sola çarpık durummda ise olduğundan az tahmin edilebilir. Bunu engellemek için dağılımın loaritması alınır ve dağılım normal dağılıma yaklaştırılır. Yukarıdaki görselde bazı dağılımlara ait % kümülatif frekans (Kf) eğrileri ve histogramlar verilmiştir.
Bunlardan, a ve b- anlamsız yani veri çok az; c- normal ya da simetrik dağılım; d- iki farklı örnek seti bir arada (bunlardan biri sağa diğeri sola çarpık dağılımlı olup, dönüm noktası, saptandıktan sonra iki ayrı topluluğa ayrılmalıdır); e- sağa çarpık ya da pozitif çarpık dağılım;
f- sola çarpık ya da negatif çarpık dağılım (e ve f durumunda verilerin logaritması alınarak ya da farklı yöntemler uygulanarak normal dağılıma yaklaşılır); g- örneklemenin yetersiz olduğu normal dağılım veya iki farklı örnek setini işaret eder (örnek miktarı arttırılarak kontrol edilmelidir).
Normal dağılımlara ait histogram ve frekans eğrileri
Normal dağılım gösteren verilerin sınıflanmasından sonra çizilen kutucukların tepe orta noktalarının birleştirilmesiyle elde edilen eğri bir çan eğrisine benzer. Bu çan eğrisini ortadan iki eşit parçaya bölen çizginin, x eksenini (değişkene ait değerleri temsil eden eksen) kestiği nokta verilerin ortalamasını, medyanını ve modunu gösterir.
Logaritmik dağılımlara ait histogram ve frekans eğrileri
Veriler normal dağılıma uymuyorsa, sağa ya da sola çarpık dağılım gösterirler. Bu durumda bireysel verilerin logaritmik çevrimi sonucunda elde edilen yeni veriler log normal dağılım gösterebilirler. Sağa çarpıklık, normal veri aralığı dışında, birkaç anormal yüksek değerin bulunmasından kaynaklanır. Sola çarpık durumda ise tersi söz konusudur.
Maden yataklarında daha ziyade sağa çarpık durumlar söz konusudur. Bu durumda mod küçük değerlerde bulunurken, ortalama değer aşağıdaki görselde olduğu gibi en sağda yer alır. Medyan ise her zaman ortada bulunur. Logaritmik verilerin ortalamasının antilog‘u geometrik ortalamayı verir. Geometrik ortalama çarpık dağılımlardan en anlamlı sonucu belirtir.
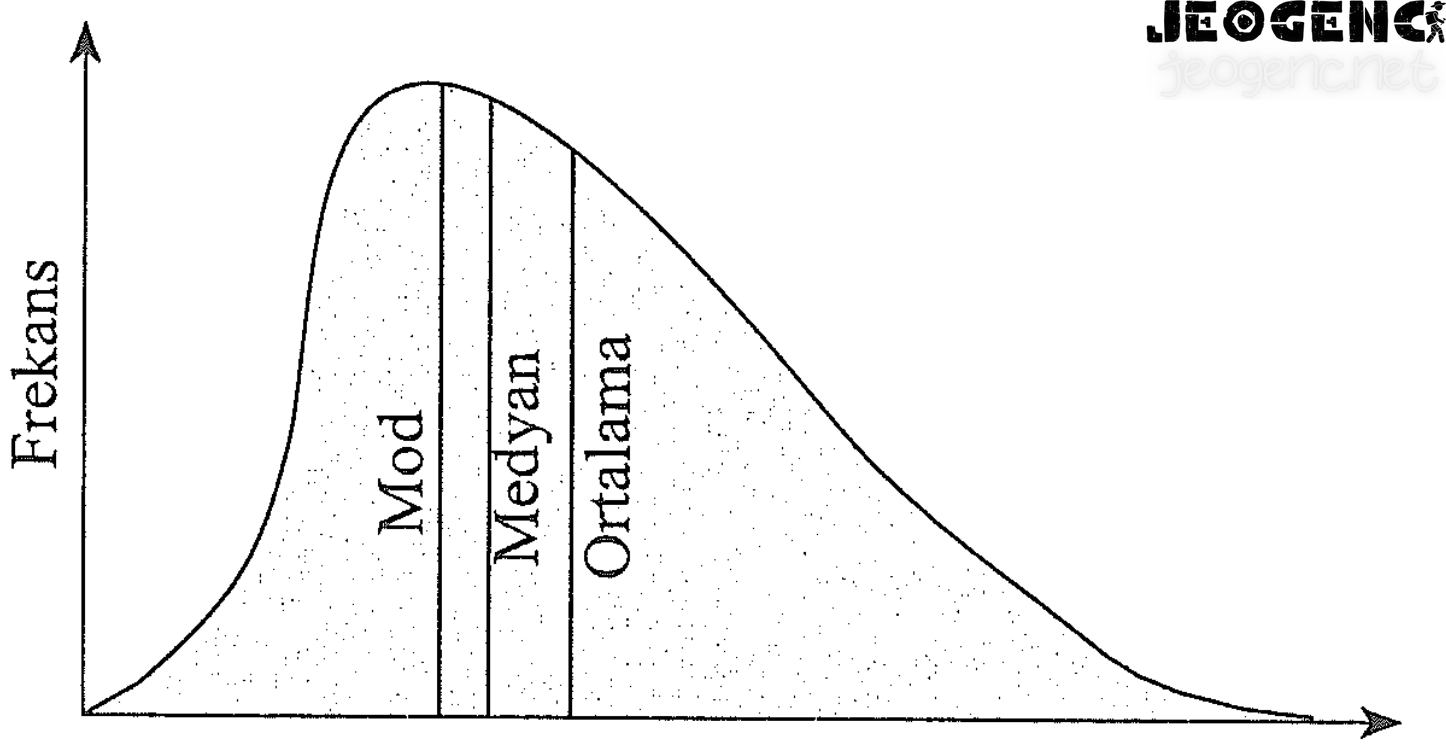
Log-normal dağılımın özellikleri
- Çan eğrisi sağa çarpıktır.
- Verilerin logaritması, geometrik ortalamanın doğal logaritması (In) etrafında normal dağılım gösterir.
- Geometrik ortalama (GO) = Medyan = logaritmik değerlerin ortalamasının antilog’udur.
- Logaritmik standart sapma ise grafiksel olarak aşağıdaki şekilde hesaplanır.
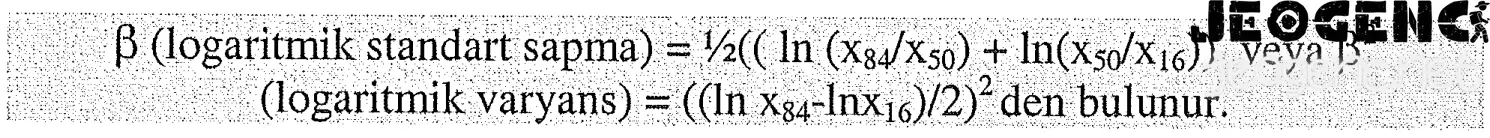
Dairesel Grafikler
Dairesel grafikler, kategorik verilerin dağılımını göstermek için kullanılır. Her kategori, dairenin bir dilimini temsil eder ve dilimlerin büyüklüğü, kategorilerin frekanslarına orantılıdır.
Daha ziyade süreksiz verilerin sunumunda kullanılırlar. Dairesel grafikler iki ya da daha fazla benzer veri setinin karşılaştırılmasında oldukça kullanışlıdır. Burada alan frekanslara göre orantılanır. Diyagram yada grafik ya %100’e ya da 360 derecelik açıya göre hazırlanır.
Dairesel grafiklerin kullanım alanları
- Kategorik verilerin dağılımını göstermek: Dairesel grafikler, jeolojik verilerin kategorik özelliklerini görselleştirmek için kullanılır. Örneğin, bir kayaç örneğindeki mineral bileşimlerinin dağılımını veya bir jeolojik haritadaki kayaç türlerinin dağılımını dairesel grafiklerle gösterebilirsiniz.
- Farklı kategorileri karşılaştırmak: Dairesel grafikler, farklı kategorileri görsel olarak karşılaştırmak için kullanılabilir. Örneğin, farklı jeolojik birimlerin kayaç türlerinin dağılımlarını veya farklı jeokimyasal elementlerin konsantrasyonlarını dairesel grafiklerle karşılaştırabilirsiniz.
- Veri setindeki eğilimleri ve örüntüleri görselleştirmek: Dairesel grafikler, veri setindeki eğilimleri ve örüntüleri görselleştirmek için kullanılabilir. Örneğin, zamana bağlı olarak bir jeolojik olayın değişimini veya farklı jeolojik ortamlarda bir jeokimyasal elementin konsantrasyon değişimini dairesel grafiklerle gösterebilirsiniz.
Dikkat edilmesi gereken bazı noktalar
- Kategoriler sayısı: Dairesel grafiklerde çok fazla kategori kullanmamak gerekir. Çok fazla kategori kullanıldığında, grafik karmaşık hale gelir ve yorumlanması zorlaşır.
- Renk kullanımı: Dairesel grafiklerde renkler, kategorileri ayırt etmek için kullanılır. Renklerin dikkatli seçilmesi ve farklı kategoriler için farklı renklerin kullanılması önemlidir.
- Başlık ve etiketler: Dairesel grafiklerin açıklayıcı bir başlığı ve etiketleri olması gerekir. Başlık, grafiğin neyi gösterdiğini açıkça belirtmelidir. Etiketler ise, her dilimin hangi kategoriyi temsil ettiğini açıkça belirtmelidir.
Kutu Grafikleri
Kutu grafikleri, bir veri setinin dağılımı ve değişkenliği hakkında hızlı bir şekilde bilgi edinmek için kullanılan grafiklerdir. Bir kutu grafiği, bir dikey çizgi ve bu çizginin üzerinde ve altında uzanan bir kutu şeklinde gösterilir.
Verilerin anlaşılması ve incelenmesinde kullanılan pratik bir diğer gösterim şekli ise dağılımın merkezini ve yayılımını gösteren kutu grafiğidir. Bu grafik yardımıyla aynı zamanda verilerin asimetrisi, kümelenmeleri ve uç değerleri aşağıdaki görselde olduğu gibi kolaylıkla görülür. Diyagramın ortasındaki kutu verilerin %25 ila %75’ini içerir. Ortasındaki çizgi ise %50’inci değer, yani medyan değeridir. Eğer bu çizgi kutunun tam ortasında ise, dağılım simetriktir. Merkezden uzaklaşan medyan asimetriyi gösterir.
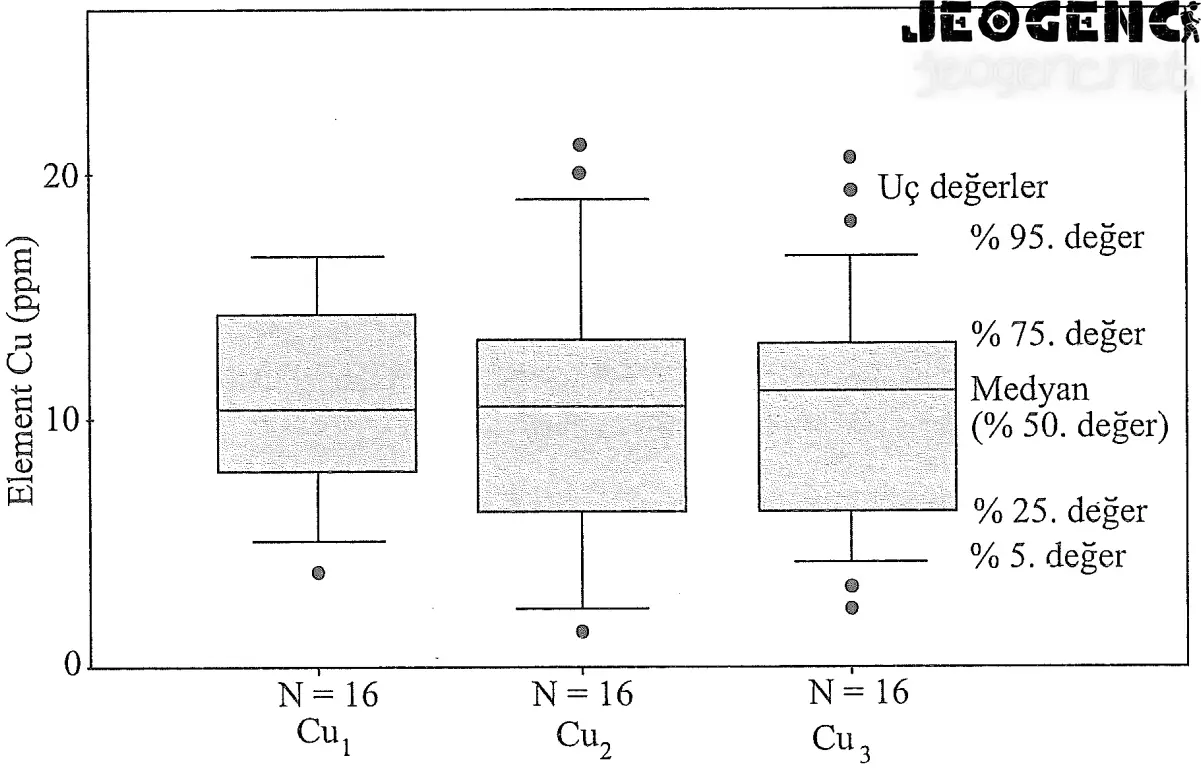
Medyan alt değerlere daha yakın ise, sağa çarpık bir dağılımdan bahsedilir. Kutuya he iki tarafından çizilen dik çizgilerin en uç noktası kutunun yüksekliğini 3/2’si kadar olup, kutu ve bu çizgiler tüm verilerin %90’ını içerir. Kutunun her iki tarafındaki çizgilerin eşit uzunlukta olması simetrik bir dağılımı gösterir. Dik çizgilerin uzunluğunun kutunun yüksekliğinin 3/2’sinden kısa veya daha uzun olması, basık ya da sivri dağılımları gösterir. Bu grafiğin en büyük eksikliği örnek sayısı hakkında bilgi vermemesidir.
Kutu grafiklerinin bileşenleri
- Medyan: Medyan, veri setinin tam ortasındaki değeri temsil eder. Kutu grafiğinde, medyan dikey çizginin tam ortasında yer alır.
- Birinci ve üçüncü çeyrek: Birinci ve üçüncü çeyrek, veri setinin sırasıyla %25’ini ve %75’ini temsil eder. Birinci ve üçüncü çeyrek değerleri, dikey çizginin üzerinde ve altında yer alan kutunun kenarlarını belirler.
- Minimum ve maksimum değerler: Minimum ve maksimum değerler, veri setinin en küçük ve en büyük değerlerini temsil eder. Kutu grafiğinde, minimum ve maksimum değerler, dikey çizginin alt ve üst ucunda yer alan bıyıklar ile gösterilir.
Kutu grafiklerinin kullanım alanları
- Farklı veri setlerini karşılaştırmak: Kutu grafikleri, farklı veri setlerinin dağılımlarını ve değişkenliklerini karşılaştırmak için kullanılabilir. Örneğin, farklı jeolojik birimlerin kayaç türlerinin dağılımlarını veya farklı jeokimyasal elementlerin konsantrasyonlarını kutu grafiklerle karşılaştırabilirsiniz.
- Veri setlerindeki aşırı değerleri tespit etmek: Kutu grafiklerindeki bıyıklar, veri setindeki aşırı değerleri tespit etmek için kullanılabilir. Aşırı değerler, kutunun dışına uzanan bıyıklar ile gösterilir.
- Veri setlerindeki eğilimleri ve örüntüleri görselleştirmek: Kutu grafikleri, veri setlerindeki eğilimleri ve örüntüleri görselleştirmek için kullanılabilir. Örneğin, zamana bağlı olarak bir jeolojik olayın değişimini veya farklı jeolojik ortamlarda bir jeokimyasal elementin konsantrasyon değişimini kutu grafiklerle gösterebilirsiniz.
Dikkat edilmesi gereken bazı noktalar
- Y ekseninin ölçeği: Y ekseninin ölçeği, veri setinin dağılımına göre seçilmelidir. Y ekseninin ölçeği uygun şekilde seçilmezse, kutu grafiği yorumlamak zor olabilir.
- Bıyıkların uzunluğu: Bıyıkların uzunluğu, aşırı değerlerin tanımlanmasına göre seçilmelidir. Bıyıklar çok uzun veya çok kısa seçilirse, kutu grafiği yorumlamak zor olabilir.
- Renk kullanımı: Kutu grafiklerinde renkler, farklı veri setlerini veya farklı kategorileri ayırt etmek için kullanılabilir. Renklerin dikkatli seçilmesi ve farklı veri setleri veya kategoriler için farklı renklerin kullanılması önemlidir.
