Regresyon nedir? Bir regresyon analizi size ne anlatır?

Regresyon, bir bağımlı değişken (genellikle Y ile gösterilir) ve bir dizi başka değişken (bağımsız değişkenler olarak bilinir) arasındaki ilişkinin gücünü ve karakterini belirlemeye çalışan finans, yatırım ve diğer disiplinlerde kullanılan istatistiksel bir yöntemdir.

Analizinin iki ana tipi vardır: basit regresyon ve çoklu regresyon. Basit regresyon, bir bağımlı değişkenin değerini, bir bağımsız değişkenin değerine göre tahmin etmek için kullanılır. Çoklu regresyon, birden fazla bağımsız değişkenin değerini kullanarak bir bağımlı değişkenin değerini tahmin etmek için kullanılır.

Regresyon analizinin temelleri:

Regresyon analizi, iki değişken arasındaki ilişkiyi ölçmek ve tahmin etmek için kullanılan bir istatistiksel yöntemdir. Bağımlı değişkenin (y) değerini, bağımsız değişkenin (x) değerine göre tahmin etmek için kullanılır.

Bir regresyon analizi size ne anlatır?

Bir dizi bağımsız değişken ile bağımlı değişken arasındaki ilişkileri tanımlamak için regresyon analizini kullanılır. Regresyon analizi, katsayıların her bağımsız değişken ile bağımlı değişken arasındaki ilişkiyi temsil ettiği bir regresyon denklemi üretir.

Regresyon analizi, aşağıdakileri anlamanıza yardımcı olabilir:

Bağımsız değişken, bağımlı değişkeni ne kadar etkiliyor?
Bağımsız değişkenin bağımlı değişken üzerindeki etkisi nasıl değişiyor?
Bağımlı değişkenin gelecekteki değerlerini nasıl tahmin edebiliriz?

Regresyon analizinin sonuçları, bir grafik veya tablo şeklinde sunulabilir. Grafik, bağımlı ve bağımsız değişken arasındaki ilişkiyi görsel olarak gösterir. Tablo ise, regresyon modelinin katsayılarını ve diğer önemli bilgileri gösterir.

Regresyon analizi ne için kullanılır?

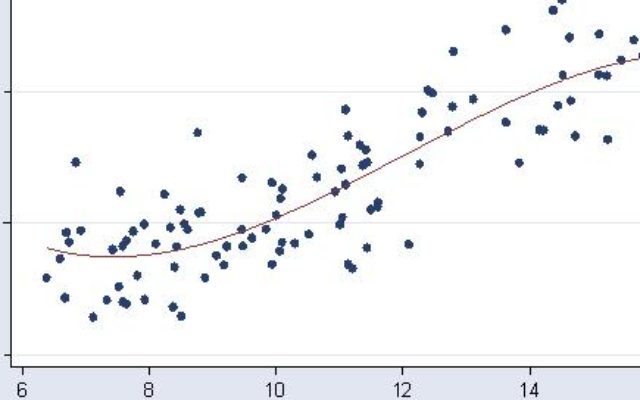
Hangi değişkenlerin ilgi konusu bir konu üzerinde etkisi olduğunu belirlemenin güvenilir bir yöntemidir. Gerçekleştirme süreci, hangi faktörlerin en önemli olduğunu, hangi faktörlerin göz ardı edilebileceğini ve bu faktörlerin birbirini nasıl etkilediğini güvenle belirlemenize olanak tanır.

İki ana tipi vardır: basit regresyon ve çoklu regresyon. Basit regresyon, bir bağımlı değişkenin değerini, bir bağımsız değişkenin değerine göre tahmin etmek için kullanılır. Çoklu regresyon, birden fazla bağımsız değişkenin değerini kullanarak bir bağımlı değişkenin değerini tahmin etmek için kullanılır.

Regresyon analizi, birçok farklı alanda kullanılabilen güçlü bir araçtır. Örneğin, regresyon analizi aşağıdakiler için kullanılabilir:

Fiyat tahmini: Regresyon analizi, bir ürünün veya hizmetin fiyatının, geçmiş verilere göre nasıl değişeceğini tahmin etmek için kullanılabilir.
Talep tahmini: Regresyon analizi, bir ürünün veya hizmetin talebinin, geçmiş verilere göre nasıl değişeceğini tahmin etmek için kullanılabilir.
Risk analizi: Regresyon analizi, bir olayın gerçekleşme olasılığını tahmin etmek için kullanılabilir. Örneğin, bir şirketin iflas etme olasılığını veya bir hastanın belirli bir hastalığı kapma olasılığını tahmin etmek için regresyon analizi kullanılabilir.

Pazarlama etkisinin ölçülmesi: Regresyon analizi, bir pazarlama kampanyasının satışları veya müşteri memnuniyetini nasıl etkilediğini ölçmek için kullanılabilir.
Eğitim başarısının tahmin edilmesi: Regresyon analizi, bir öğrencinin notlarının, ders çalışma saatleri veya diğer faktörlere göre nasıl değişeceğini tahmin etmek için kullanılabilir.

Regresyon analizi, veri kümenizdeki iki değişken arasındaki ilişkiyi anlamlandırmanıza ve bu ilişkiyi kullanarak gelecekteki değerleri tahmin etmenize yardımcı olabilir.

Regresyon örneği nedir?

Örneğin; yaş, cinsiyet ve diyetin (öngörücü değişkenler) boy (sonuç değişkeni) üzerindeki göreceli etkilerini ölçmek için kullanılabilir. Doğrusal regresyon, çoklu regresyon, çok değişkenli regresyon, sıradan en küçük kareler (OLS) ve regresyon olarak da bilinir.

Regresyon analizinin bir örneği, bir işletmenin satışlarının, pazarlama bütçesinin büyüklüğüne göre nasıl değiştiğini tahmin etmek olabilir. Bu durumda, bağımlı değişken satışlar (y) ve bağımsız değişken pazarlama bütçesi (x) olacaktır. Regresyon analizi kullanılarak, pazarlama bütçesinin büyüklüğünün satışları nasıl etkilediğini tahmin etmek için bir model oluşturulabilir.

Bir başka örnek, bir öğrencinin notlarının, ders çalışma saatlerine göre nasıl değiştiğini tahmin etmek olabilir. Bu durumda, bağımlı değişken notlar (y) ve bağımsız değişken ders çalışma saatleri (x) olacaktır. Regresyon analizi kullanılarak, ders çalışma saatlerinin notları nasıl etkilediğini tahmin etmek için bir model oluşturulabilir.

En İyi Regresyon Modelini Bulmak İçin İstatistiksel Yöntemler

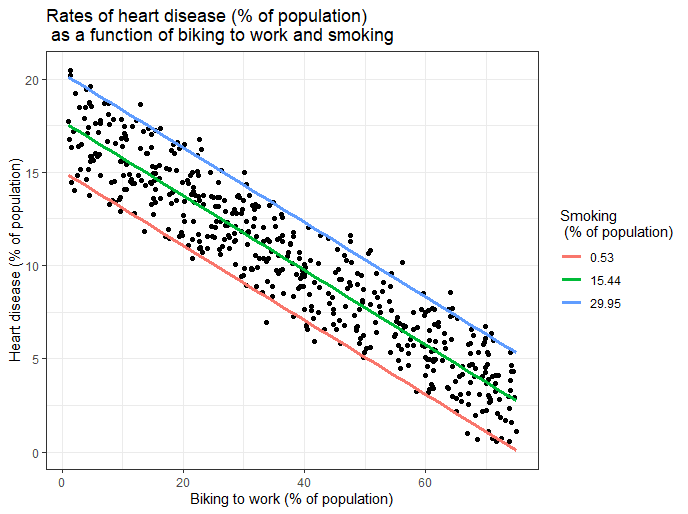
Düzeltilmiş R-kare ve Öngörülen R-kare: Genel olarak, daha yüksek ayarlanmış ve tahmini R-kare değerlerine sahip modelleri seçersiniz.
Yordayıcılar için P değerleri: Regresyonda, düşük p değerleri istatistiksel olarak anlamlı olan terimleri gösterir.

En iyi regresyon modelini bulmak için kullanılan bazı istatistiksel yöntemler şunlardır:

Geriye doğru eleme: Geriye doğru eleme, modelde bulunan bağımsız değişkenleri, modelin performansını en az etkileyen değişkenlerden başlayarak kaldırma işlemidir. Bu yöntem, modelin karmaşıklığını azaltmaya ve model performansını iyileştirmeye yardımcı olur.
İleriye doğru seçim: İleriye doğru seçim, modelde bulunmayan bağımsız değişkenleri, modelin performansını en çok iyileştiren değişkenlerden başlayarak ekleme işlemidir. Bu yöntem, modelin performansını iyileştirmeye yardımcı olur.

Lasso: Lasso, bağımsız değişkenlerin katsayılarını azaltarak modelin karmaşıklığını azaltan bir yöntemdir. Lasso yöntemi, çoklu doğrusal regresyon modellerinde kullanılan bir tekniktir.

Bu yöntemler, veri kümenizin özelliklerine ve ihtiyaçlarınıza göre kullanılabilir.

Bir regresyon modelinin uygun olup olmadığını nasıl anlarsınız?

En iyi uyum çizgisi, gerçek ve tahmin edilen sonuçlar arasındaki kare farkların toplamını en aza indirendir. Minimum kare fark toplamının ortalamasını almak, Ortalama Kare Hata (MSE) olarak bilinir. Değer ne kadar küçükse, regresyon modeli o kadar iyidir.

Bir regresyon modelinin uygun olup olmadığını anlamak için, modelin performansını değerlendirebilirsiniz. Modelin performansını değerlendirmek için kullanılan bazı yaygın ölçütler şunlardır:

R-kare: R-kare, bağımlı değişkenin varyansının ne kadarının bağımsız değişkenler tarafından açıklandığını gösteren bir ölçüttür. R-kare değeri ne kadar yüksek olursa, modelin performansı o kadar iyi olur.

Standart hata: Standart hata, tahminlerin varyansını gösteren bir ölçüttür. Standart hata değeri ne kadar düşük olursa, tahminler o kadar güvenilir olur.
Hataların ortalama karesi: Hataların ortalama karesi, tahmin hatalarının ortalamasını gösteren bir ölçüttür. Hataların ortalama karesi değeri ne kadar düşük olursa, modelin performansı o kadar iyi olur.

Bu ölçütleri kullanarak, regresyon modelinizin performansını değerlendirebilir ve modelinizin iyi bir şekilde uygun olup olmadığını belirleyebilirsiniz.

Nasıl iyi bir regresyon modeli yaparsınız?

Regresyon katsayılarının marjinal sonuçlar olduğunu unutmayın.

Tek değişkenli tanımlamalar ve grafiklerle başlayın.
Daha sonra, yine grafikler dahil olmak üzere iki değişkenli tanımlayıcıları çalıştırın.
Setlerdeki yordayıcıları düşünün.

Model oluşturma ve sonuçları yorumlama el ele gider.

İyi bir regresyon modeli yapmak için aşağıdaki adımları takip edebilirsiniz:

Verilerinizi toplayın. Regresyon analizi yapabilmek için, bağımlı ve bağımsız değişkenlerinizi içeren bir veri kümesine ihtiyacınız vardır. Bu veri kümesi, mümkün olduğunca büyük ve çeşitli olmalıdır.
Verilerinizi inceleyin. Verilerinizi inceleyerek, bağımsız ve bağımlı değişkenler arasındaki ilişkiyi anlamaya çalışın. Bu ilişkiyi anlamak, daha doğru bir regresyon modeli oluşturmanıza yardımcı olacaktır.
Regresyon modelinizi oluşturun. Verilerinizi inceledikten sonra, uygun bir regresyon modelini seçebilirsiniz. Basit regresyon veya çoklu regresyon kullanabilirsiniz.

Regresyon modelinizi değerlendirin. Regresyon modelinizi oluşturduktan sonra, modelinizin performansını değerlendirmeniz gerekir. Bu değerlendirmeyi, R-kare, standart hata ve hataların ortalama karesi gibi ölçütler kullanarak yapabilirsiniz.

İyi bir regresyon modeli oluşturmak için dikkat etmeniz gereken bazı noktalar şunlardır:

Verilerinizin kalitesi önemlidir. Verileriniz hatasız ve eksiksiz olmalıdır.
Bağımsız ve bağımlı değişkenleriniz arasında bir ilişki olmalıdır. Bu ilişkiyi anlamak, daha doğru bir regresyon modeli oluşturmanıza yardımcı olacaktır.
Regresyon modelinizin karmaşıklığı, veri kümenizin boyutuna ve karmaşıklığına uygun olmalıdır. Çok karmaşık bir model, veri kümeniz için fazla olabilir ve bu da modelinizin performansını düşürebilir.

Regresyon analizi, iki değişken arasındaki ilişkiyi ölçmek ve tahmin etmek için kullanılan güçlü bir araçtır. İyi bir regresyon modeli oluşturmak için yukarıdaki adımları takip ederek, veri kümeniz için en uygun modeli bulabilirsiniz.

İşte iyi bir regresyon modeli oluşturmanıza yardımcı olabilecek bazı ek ipuçları:

Regresyon modelinizi oluştururken, veri kümenizden bir test kümesi ayırın. Test kümesini, modelinizin performansını değerlendirmek için kullanın.
Regresyon modelinizi oluştururken, farklı modeller deneyin. Farklı modellerin performansını karşılaştırarak, sizin için en iyi modeli bulabilirsiniz.

Regresyon modelinizi oluşturduktan sonra, modelinizin performansını düzenli olarak izleyin. Modelinizin performansı değişirse, modelinizi güncellemeniz gerekebilir.

Regresyon nasıl hesaplanır?

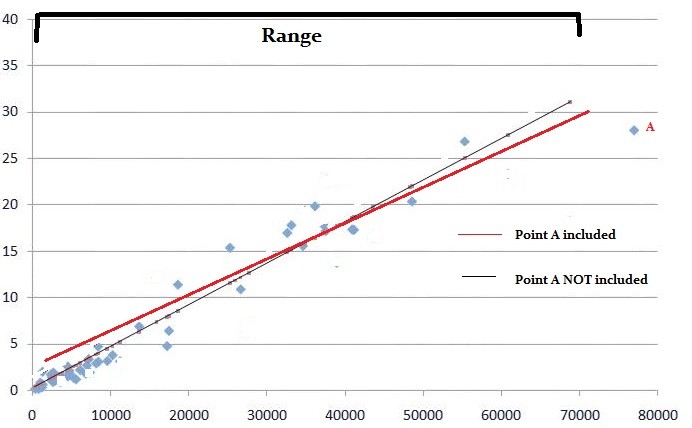
En iyi uyan çizgi (veya regresyon çizgisi) için formül y = mx + b‘dir, burada m, doğrunun eğimidir ve b, y kesişim noktasıdır.

İki değişken arasındaki ilişkiyi ölçmek ve tahmin etmek için kullanılan bir istatistiksel yöntemdir. Regresyon analizi, bağımlı değişkenin (y) değerini, bağımsız değişkenin (x) değerine göre tahmin etmek için kullanılır.

Basit regresyonda regresyon doğrusu, y = a + bx şeklinde ifade edilir. Burada, a ve b, doğrunun katsayılarını temsil eder.

En küçük kareler yöntemi, basit regresyonda regresyon doğrusunu bulmak için kullanılan bir yöntemdir. Bu yöntem, bağımlı değişkenin (y) gözlem değerleri ile regresyon doğrusunun kesişme noktaları arasındaki mesafelerin kareleri toplamını minimum yapan doğruyu bulmaya çalışır.

Regresyonu elle nasıl hesaplarsınız?

X değişkeninizin ortalamasını hesaplayın.
Her X ile ortalama X arasındaki farkı hesaplayın.
Farklılıkları giderin ve hepsini toplayın.

Y değişkeninizin ortalamasını hesaplayın.
Farkları (X ve Y’nin kendi ortalamalarından) çarpın ve hepsini toplayın.

En küçük kareler ilkesi nedir?

En küçük kareler ilkesi, bağımlı değişkeninizin gözlemlenen değerleri ile SRF’nizden tahmin edilen değerler arasındaki mesafenin karesi toplamının en aza indirilmesi için (mümkün olan en küçük değer) SRF’nin (sabit ve eğimli değerlerle) oluşturulması gerektiğini belirtir.

İki değişken arasındaki ilişkiyi tahmin etmek için kullanılan bir yöntemdir. Bu yöntem, bağımlı değişkenin (y) değerini, bağımsız değişkenin (x) değerine göre tahmin etmek için kullanılan bir matematiksel fonksiyon olan en küçük kareler doğrusunu bulmak için kullanılır.

Aşağıdaki gibi ifade edilebilir:

En küçük kareler doğrusu, bağımlı değişkenin (y) gözlem değerleri ile en küçük kareler doğrusunun kesişme noktaları arasındaki mesafelerin karelerinin toplamını minimum yapan doğrudur.

En küçük kareler doğrusunu nasıl bulursunuz?

Her (x, y) noktası için x ² ve xy’yi hesaplayın.
Tüm x, y, x ² ve xy’yi toplayın, bu da bize Σx, Σy, Σx ² ve Σxy’yi verir (Σ, “topla” anlamına gelir)

Eğimi hesaplayın
m = N Σ (xy) – Σx Σy N Σ (x ² ) – (Σx) ²
: Kesişimi Hesaplayın

b = Σy – m Σx N.
Bir çizginin denklemini oluşturun.

En küçük kareler doğrusu, bir bağımlı değişkenin (y) değerini, bağımsız değişkenin (x) değerine göre tahmin etmek için kullanılan bir matematiksel fonksiyondur. Bu fonksiyon, y = a + bx şeklinde ifade edilir. Burada, a ve b, doğrunun katsayılarını temsil eder. En küçük kareler doğrusunu bulmak için, aşağıdaki normal denklemleri çözmek gerekir:

n * a + b * sum(x) = sum(y)
b * sum(x^2) + n * b * sum(x) = sum(x * y)

Bu denklemler, y = a + bx doğrusu üzerindeki (xi, yi) noktaları ile verilen (xi, yi) noktaları arasındaki uzaklıkların kareleri toplamını minimum yapan a ve b katsayılarını verir.

Normal denklemleri çözmek için, aşağıdaki formüller kullanılabilir:

a = (sum(y) - b * sum(x)) / n
b = (sum(x * y) - sum(x) * sum(y)) / (sum(x^2) - n * sum(x)^2)

En küçük karelerin doğrusunu bulma çözümü

Örneğin, aşağıdaki veri kümesi için en küçük kareler doğrusunu bulalım:

x | y
---|---
1 | 2
2 | 4
3 | 6
4 | 8

Bu veri kümesi için, normal denklemler aşağıdaki gibi çözülür:

a = (2 + 4 + 6 + 8) / 4 – b * (1 + 2 + 3 + 4) / 4 = 10 – b / 2 b = ((1 * 2 + 2 * 4 + 3 * 6 + 4 * 8) – (1 + 2 + 3 + 4) * (2 + 4 + 6 + 8)) / ((1^2 + 2^2 + 3^2 + 4^2) – 4 * (1 + 2 + 3 + 4)^2) = 20 – 28 / 16 = -1 / 4

Buradan, a = 10 ve b = -1/4 olduğu sonucuna varılır. Bu sonuçlar, y = 10 – x/4 şeklinde ifade edilen en küçük kareler doğrusunu verir.

Korelasyon ve regresyon arasındaki fark nedir?

Korelasyon, her iki değişkenin birlikte hareket etme derecesini belirler. Bununla birlikte, regresyon değişikliğin etkisini belirtir. İçinde birim olarak değerlendirilir. Değişken (q) üzerinde bilinen değişken (s). Korelasyon, iki değişken arasındaki bağlantıyı kurmaya yardımcı olur. Korelasyon ve regresyon, iki veya daha fazla değişken arasındaki ilişkiyi inceleyen iki istatistiksel yöntemdir. Ancak, her iki yöntemin de farklı amaçları ve uygulamaları vardır.

Korelasyon analizi, iki değişken arasındaki ilişkinin gücünü ve yönünü ölçer. Korelasyon katsayısı, -1 ile 1 arasında değişen bir sayı ile ifade edilir. 1, iki değişken arasında mükemmel bir doğrusal ilişki olduğunu gösterir. -1, iki değişken arasında mükemmel bir ters doğrusal ilişki olduğunu gösterir. 0, iki değişken arasında hiçbir ilişki olmadığını gösterir.

Regresyon analizi, bir değişkenin (bağımlı değişken) değerinin, diğer bir değişkenin (bağımsız değişken) değerine göre nasıl tahmin edilebileceğini belirler. Regresyon doğrusu, bağımlı değişkenin değerini bağımsız değişkenin değerine göre tahmin etmek için kullanılan bir matematiksel fonksiyondur.

Korelasyon ve regresyon arasındaki temel farklar aşağıdaki gibi özetlenebilir:

Özellik	Korelasyon	Regresyon
Amaç	İki değişken arasındaki ilişkinin gücünü ve yönünü ölçmek	Bir değişkenin değerinin, diğer bir değişkenin değerine göre nasıl tahmin edilebileceğini belirlemek
Kullanılan sayısal değer	Korelasyon katsayısı (-1 ile 1 arasında değişir)	Regresyon katsayıları (bağımsız değişkenin bir birim artmasının bağımlı değişken üzerinde ne kadar etkisi olacağını gösterir)
İlişki yönüne bakılır mı?	Hayır	Evet
Tahmin yapılır mı?	Hayır	Evet