Bilimsel araştırmalarda ve günlük yaşamda, iki değişken arasındaki ilişkiyi anlamak oldukça önemlidir. Bu ilişkiyi belirlemek için kullanılan istatistiksel bir yöntem ise korelasyondur. Peki, korelasyon nedir, nasıl analiz edilir, özellikleri nelerdir ve nasıl hesaplanır? Bu yazıda, bu soruların kapsamlı yanıtlarını bulacaksınız.

Korelasyon Nedir?

Korelasyon, iki rassal değişken arasındaki doğrusal ilişkinin yönünü ve gücünü gösteren bir istatistiksel ölçüdür. Rasel değişkenler, rastgele değerler alan değişkenlerdir. Örneğin, bir öğrencinin sınav notu ve çalışma süresi rassal değişkenler olarak kabul edilebilir. Korelasyon, iki değişkenin birlikte nasıl değiştiğini ve birinin diğerini ne kadar etkilediğini belirlemede kullanılır. Basitçe ifade etmek gerekirse, korelasyon bize iki değişkenin ne kadar birbirleriyle uyumlu olduğunu gösterir.

Korelasyon Çeşitleri

İki değişken arasındaki ilişkinin yönüne göre üç çeşide ayrılır:

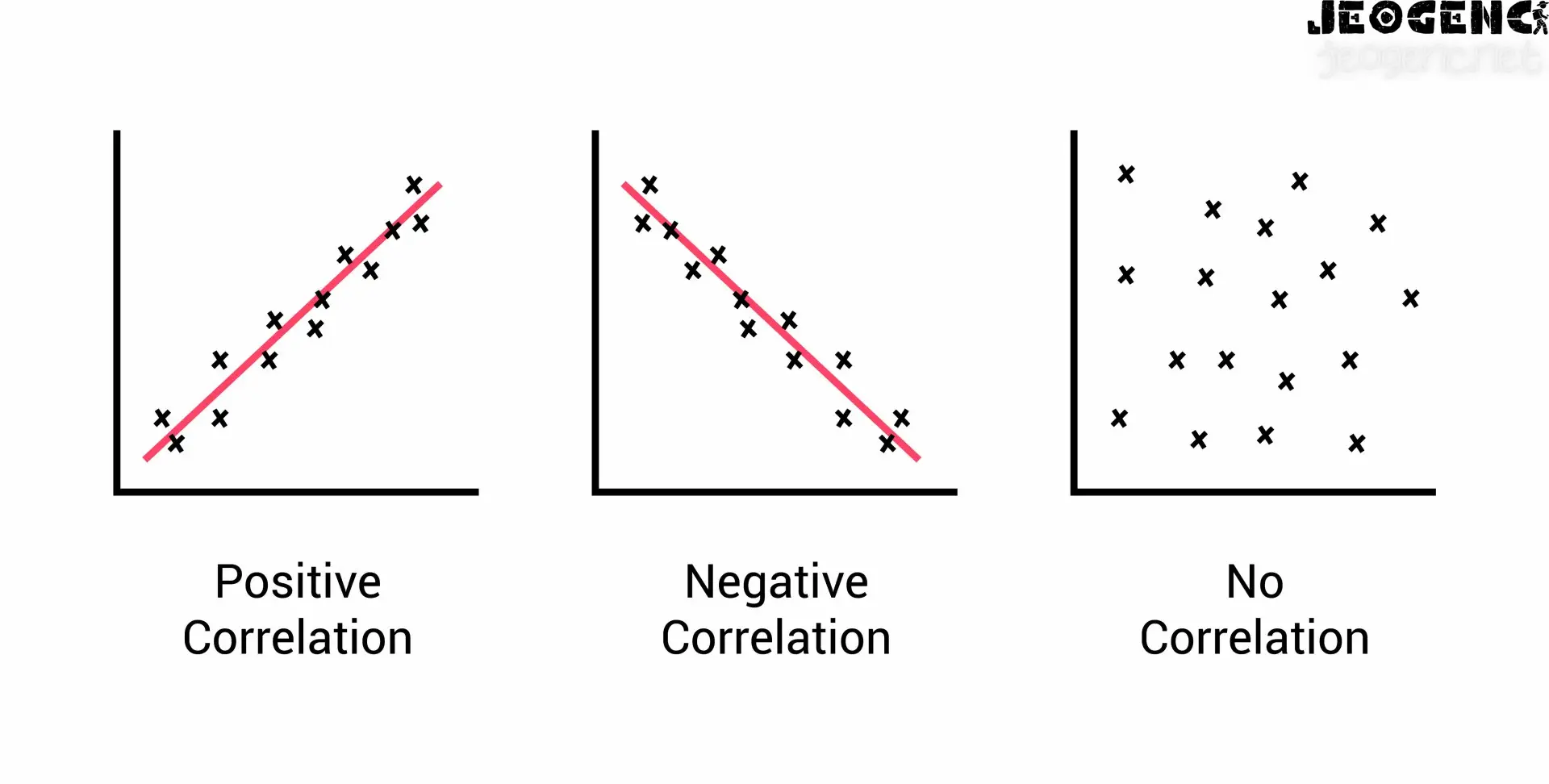
Pozitif Korelasyon

Pozitif Korelasyon Nedir?

İki değişkenin aynı yönde değiştiği durumlarda ortaya çıkar. Bu, bir değişkenin değerinin artmasıyla diğer değişkenin değerinin de artması veya bir değişkenin değerinin azalmasıyla diğer değişkenin değerinin de azalması anlamına gelir. Basitçe ifade etmek gerekirse, pozitif korelasyonda iki değişken birbirleriyle uyumlu hareket eder. Bir değişkendeki değişim, diğer değişkeni de aynı yönde etkiler.

Pozitif Korelasyon Örnekleri

Eğitim ve Gelir: Bir kişinin eğitim seviyesinin artmasıyla birlikte gelirinin de artması genellikle pozitif bir korelasyon gösterir.

Çalışma Süresi ve Verimlilik: Bir çalışanın çalışma süresinin artmasıyla birlikte iş yerindeki verimliliğinin de artması pozitif bir korelasyon örneğidir.
Yaş ve Boy: Bir kişinin yaşı arttıkça boyunun da uzaması doğal bir gelişim sürecidir ve pozitif bir korelasyon gösterir.

Pozitif Korelasyonun Yorumlanması

Pozitif korelasyon katsayısı, iki değişken arasındaki ilişkinin gücünü gösteren bir sayıdır. Bu katsayı 0 ile +1 arasında bir değer alır.

+1: Tam pozitif korelasyon (iki değişken mükemmel bir şekilde aynı yönde hareket eder)
0: Sıfır korelasyon (iki değişken arasında herhangi bir doğrusal ilişki yoktur)

Katsayının mutlak değeri ne kadar büyükse, iki değişken arasındaki ilişki o kadar güçlü demektir. Örneğin, 0.8 pozitif korelasyon katsayısı, 0.3 pozitif korelasyon katsayısına göre daha güçlü bir ilişkiye işaret eder.

Ancak, pozitif korelasyonun nedensellik anlamına gelmediğini unutmamak önemlidir. İki değişken arasında yüksek pozitif korelasyon olsa bile, birinin diğerine neden olduğunu söylemek mümkün değildir. Örneğin, eğitim ve gelir arasında pozitif bir korelasyon olsa da, bu durum eğitimin gelire neden olduğunu göstermez. Eğitim ve geliri etkileyen başka faktörler de olabilir.

Pozitif Korelasyonun Sınırlamaları

Doğrusal İlişkiler: Pozitif korelasyon analizi, sadece doğrusal ilişkileri gösterebilir. İki değişken arasında bir ilişki varsa, korelasyon katsayısı bu ilişkiyi doğru bir şekilde yansıtmayabilir.

Veri Dağılımı: Korelasyon analizi, veri setinin dağılımına duyarlıdır. Veriler normal dağılımda değilse, korelasyon katsayısı hatalı olabilir.
Nedensellik: Pozitif korelasyon, nedensellik anlamına gelmez. İki değişken arasında yüksek korelasyon olsa bile, birinin diğerine neden olduğunu söylemek mümkün değildir.

Negatif Korelasyon

Negatif Korelasyon Nedir?

İki değişkenin ters yönde değiştiği durumlarda ortaya çıkar. Bu, bir değişkenin değerinin artmasıyla diğer değişkenin değerinin azalması veya bir değişkenin değerinin azalmasıyla diğer değişkenin değerinin artması anlamına gelir. Basitçe ifade etmek gerekirse, negatif korelasyonda iki değişken birbiriyle ters orantılı hareket eder. Bir değişkendeki değişim, diğer değişkeni zıt yönde etkiler.

Negatif Korelasyon Örnekleri

Çalışma Süresi ve Uyku Süresi: Bir kişinin çalışma süresinin artmasıyla birlikte uyku süresinin azalması negatif bir korelasyon gösterir.

Ürün Fiyatı ve Talep: Bir ürünün fiyatının artmasıyla birlikte talep hacminin azalması negatif bir korelasyon örneğidir.
Yaş ve Metabolizma Hızı: Bir kişinin yaşı arttıkça metabolizma hızının yavaşlaması doğal bir süreçtir ve negatif bir korelasyon gösterir.
Obezite ve Fiziksel Aktivite: Obezite oranlarının artmasıyla birlikte fiziksel aktivite seviyelerinin azalması negatif bir korelasyon örneğidir.

Sigara Tüketimi ve Yaşam Süresi: Sigara tüketiminin artmasıyla birlikte yaşam süresinin kısalması negatif bir korelasyon gösterir.

Negatif Korelasyonun Yorumlanması

Negatif korelasyon katsayısı, iki değişken arasındaki ilişkinin gücünü gösteren bir sayıdır. Bu katsayı 0 ile -1 arasında bir değer alır.

-1: Tam negatif korelasyon (iki değişken mükemmel bir şekilde ters yönde hareket eder)
0: Sıfır korelasyon (iki değişken arasında herhangi bir doğrusal ilişki yoktur)

Katsayının mutlak değeri ne kadar büyükse, iki değişken arasındaki ilişki o kadar güçlü demektir. Örneğin, -0.8 negatif korelasyon katsayısı, -0.3 negatif korelasyon katsayısına göre daha güçlü bir ilişkiye işaret eder.

Ancak, negatif korelasyonun nedensellik anlamına gelmediğini unutmamak önemlidir. İki değişken arasında yüksek negatif korelasyon olsa bile, birinin diğerine neden olduğunu söylemek mümkün değildir. Örneğin, çalışma süresi ve uyku süresi arasında negatif bir korelasyon olsa da, bu durum uzun çalışma saatlerinin uyku süresini kısalttığı anlamına gelmez. Başka faktörler de uyku süresini etkileyebilir.

Sıfır Korelasyon

Sıfır Korelasyon Nedir?

Bu bir değişkenin değerinin değişmesiyle diğer değişkenin değerinin herhangi bir şekilde etkilenmediği anlamına gelir. Basitçe ifade etmek gerekirse, sıfır korelasyon gösteren iki değişken birbirinden bağımsızdır. Bir değişkendeki değişim, diğer değişkeni hiç etkilemez.

Sıfır Korelasyon Örnekleri

Boy ve Göz Rengi: Bir kişinin boyunun değişmesiyle göz renginin değişmesi arasında herhangi bir ilişki yoktur.
Tercih Edilen Müzik Türü ve Sıcaklık: Bir kişinin tercih ettiği müzik türü ile hava sıcaklığı arasında herhangi bir ilişki yoktur.
Ayakkabı Bedeni ve IQ: Bir kişinin ayakkabı bedeni ile IQ’su arasında herhangi bir ilişki yoktur.

Sıfır Korelasyonun Yorumlanması

Sıfır korelasyon katsayısı 0’a eşittir. Bu, iki değişken arasında herhangi bir doğrusal ilişki olmadığını gösterir. Ancak, sıfır korelasyonun iki değişken arasında hiçbir ilişki olmadığı anlamına gelmediğini unutmamak önemlidir. Sıfır korelasyon sadece, iki değişkenin doğrusal bir şekilde ilişkili olmadığını gösterir. İki değişken arasında non-linear bir ilişki olabilir.

Sıfır Korelasyonun Sınırlamaları

Doğrusal İlişkiler: Sıfır korelasyon analizi, sadece doğrusal ilişkileri gösterebilir. İki değişken arasında bir ilişki varsa, korelasyon katsayısı bu ilişkiyi doğru bir şekilde yansıtmayabilir.
Veri Dağılımı: Korelasyon analizi, veri setinin dağılımına duyarlıdır. Veriler normal dağılımda değilse, korelasyon katsayısı hatalı olabilir.
Örneklem Büyüklüğü: Sıfır korelasyon tespit etmek için yeterli örneklem büyüklüğüne sahip olmak önemlidir. Küçük örneklem boyutlarında, gerçekte var olan bir ilişki gözden kaçabilir.

Korelasyon Analizi

Korelasyon analizi, iki değişken arasındaki ilişkinin türünü, yönünü ve gücünü inceleyen bir istatistiksel yöntemdir. Bu analiz, iki değişkenin birlikte nasıl değiştiğini ve birinin diğerini ne kadar etkilediğini belirlemek için kullanılır. Basitçe ifade etmek gerekirse, korelasyon analizi, iki değişkenin birbirleriyle ne kadar uyumlu hareket ettiğini gösterir. İki değişkenin değerleri aynı yönde mi değişiyor, ters yönde mi değişiyor, yoksa hiç mi değişmiyor? Bu soruların cevabını verir.

Korelasyon Analizi Nasıl Yapılır?

Pearson korelasyon katsayısı gibi çeşitli istatistiksel yöntemler kullanarak gerçekleştirilir. Bu yöntemler, iki değişken arasındaki ilişkinin gücünü ve yönünü sayısal olarak ifade eder.

Pearson korelasyon katsayısı, -1 ile +1 arasında bir değer alır.

+1: Tam pozitif korelasyon (iki değişken mükemmel bir şekilde aynı yönde hareket eder)
0: Sıfır korelasyon (iki değişken arasında herhangi bir doğrusal ilişki yoktur)

-1: Tam negatif korelasyon (iki değişken mükemmel bir şekilde ters yönde hareket eder)

Katsayının mutlak değeri ne kadar büyükse, iki değişken arasındaki ilişki o kadar güçlü demektir. Örneğin, +0.8 korelasyon katsayısı, +0.3 korelasyon katsayısına göre daha güçlü bir ilişkiye işaret eder.

Korelasyon Analizi Nasıl Yorumlanır?

Korelasyon katsayısına bakarak iki değişkenin nasıl ilişkili olduğunu yorumlayabiliriz.

Yüksek ve Pozitif Korelasyon: Bir değişkenin değerinin artmasıyla diğer değişkenin değerinin de artması anlamına gelir.

Yüksek ve Negatif Korelasyon: Bir değişkenin değerinin artmasıyla diğer değişkenin değerinin azalması anlamına gelir.
Düşük veya Sıfır Korelasyon: İki değişken arasında herhangi bir doğrusal ilişki olmadığı anlamına gelir.

Korelasyon Özellikleri

Korelasyon katsayısı, -1 ile +1 arasında bir değer alır.
Pozitif korelasyon, iki değişkenin aynı yönde değiştiğini gösterir.
Negatif korelasyon, iki değişkenin ters yönde değiştiğini gösterir.

Sıfır korelasyon, iki değişken arasında herhangi bir doğrusal ilişki olmadığını gösterir.
Korelasyon katsayısının büyüklüğü, ilişkinin gücünü gösterir.

Korelasyon Analizi Hesaplama

Pearson korelasyon katsayısı, iki değişken arasındaki doğrusal ilişkiyi hesaplamak için en yaygın kullanılan yöntemdir. Bu katsayı -1 ile +1 arasında bir değer alır ve iki değişkenin ne kadar uyumlu hareket ettiğini gösterir.

Korelasyon Katsayısı Nasıl Hesaplanır?

Pearson korelasyon katsayısını hesaplamak için aşağıdaki formül kullanılır:

r = Σ((xi – x̄)(yi – ȳ)) / √(Σ(xi – x̄)² * Σ(yi – ȳ)²)

Formüldeki İfadeler

r: Korelasyon katsayısı
xi: i. gözlemdeki x değeri

x̄: x değişkeninin ortalaması
yi: i. gözlemdeki y değeri
ȳ: y değişkeninin ortalaması

Σ: Toplam işaretini temsil eder

Hesaplama Aşamaları

Veri Setini Hazırlayın: İki değişken için veri setini hazırlayın. Veri seti, her iki değişken için de aynı sayıda gözleme sahip olmalıdır.

Ortalamaları Hesaplayın: Her iki değişken için de ortalama değerleri (x̄ ve ȳ) hesaplayın.
Her Gözlem için Farkları Hesaplayın: Her gözlem için x ve y değerlerini ortalamalarından çıkarın (xi – x̄ ve yi – ȳ).
Çarpımların Toplamını Hesaplayın: Her gözlem için (xi – x̄)(yi – ȳ) değerlerinin çarpımlarının toplamını hesaplayın.

Karelerin Toplamlarını Hesaplayın: Her iki değişken için de (xi – x̄)² ve (yi – ȳ)² değerlerinin karelerinin toplamlarını hesaplayın.
Formülü Uygulayın: Hesapladığınız değerleri formüle yerleştirin ve korelasyon katsayısını (r) hesaplayın.

Örnek

Aşağıdaki tabloda, 10 öğrencinin matematik ve fen bilimleri sınav notları yer almaktadır.

Öğrenci	Matematik	Fen Bilimleri
1	80	75
2	72	68
3	90	85
4	65	60
5	85	80
6	78	72
7	95	90
8	60	55
9	82	78
10	75	70

1. Adım: Veri setini hazırlayın.

2. Adım: Ortalamaları hesaplayın.

Matematik ortalaması (x̄): (80 + 72 + 90 + … + 75) / 10 = 78
Fen Bilimleri ortalaması (ȳ): (75 + 68 + 85 + … + 70) / 10 = 73

3. Adım: Her gözlem için farkları hesaplayın.

4. Adım: Çarpımların toplamını hesaplayın.

5. Adım: Karelerin toplamlarını hesaplayın.

6. Adım: Formülü uygulayın.

r = Σ((xi – x̄)(yi – ȳ)) / √(Σ(xi – x̄)² * Σ(yi – ȳ)²)

= (2 * 4 + 36 + 225 + … + 49) / √((4 + 36 + 144 + … + 49) * (4 + 9 + 25 + … + 1))

r = 400 / √(576 * 36)

= 0.82

Korelasyonun Yorumlanması

Katsayısının yorumlanması, katsayının büyüklüğüne ve yönüne bağlıdır.

Korelasyon Katsayısının Büyüklüğü

Korelasyon katsayısının mutlak değeri ne kadar büyükse, iki değişken arasındaki ilişki o kadar güçlü demektir.

|r| > 0.7: Güçlü korelasyon
0.3 < |r| < 0.7: Orta derecede korelasyon

|r| < 0.3: Zayıf korelasyon

Güçlü korelasyon, iki değişkenin birbirleriyle uyumlu şekilde değiştiği anlamına gelir. Örneğin, bir öğrencinin çalışma süresinin artmasıyla birlikte sınav notlarının da artması güçlü bir korelasyon gösterir.

Orta derecede korelasyon, iki değişken arasında belirli bir ilişki olduğunu gösterir. Ancak bu ilişki her zaman doğrusal olmayabilir.

Zayıf korelasyon, iki değişken arasında çok az veya hiç ilişki olmadığı anlamına gelir.

Korelasyon Katsayısının Yönü

Korelasyon katsayısının işareti, iki değişkenin nasıl değiştiğini gösterir.

Pozitif korelasyon (r > 0): İki değişken aynı yönde değişir. Bir değişkenin değeri arttıkça diğer değişkenin değeri de artar veya bir değişkenin değeri azaldıkça diğer değişkenin değeri de azalır.
Negatif korelasyon (r < 0): İki değişken ters yönde değişir. Bir değişkenin değeri arttıkça diğer değişkenin değeri azalır veya bir değişkenin değeri azaldıkça diğer değişkenin değeri artar.