Uzaklığa Bağlı İlişki Fonksiyonu (Variogram), iki nokta arasındaki değişkenlik ilişkisini tanımlayan bir istatistiksel araçtır. Variogram, bir değişkenin değerlerinin belirli bir uzaklıktaki diğer noktalardaki değerleriyle olan ilişkisini ölçer. Jeoloji, coğrafya, ekonomi, mühendislik ve diğer birçok alanda kullanılmaktadır.

Bölgesel değişkenlerin değerleri arasındaki fark, bu değişkenler arasındaki uzaklığın bir fonksiyonudur (Matheron, 1970; Journel, 1986). Jeoistatistikte bölgesel değişkenlerin uzaklığa bağlı değişimleri variogram fonksiyonu ile belirtilir ve bu fonksiyon birbirinden h kadar uzaktaki iki değişken arasındaki farkın varyansı olarak ifade edilir. Bir başka deyişle, iki nokta arasındaki farkın varyansının büyüklüğü noktalar arasındaki mesafenin büyüklüğüne bağlıdır.

Variogramın Özellikleri

İki temel özelliği vardır:

Variogramın simetrisi: Variogram, iki nokta arasındaki uzaklığın mutlak değerine göre simetriktir.
Variogramın monotonluğu: Variogram, uzaklığın artmasıyla artar veya azalır.

İki nokta arasındaki değişkenlik ilişkisinin her iki yöne de aynı olduğunu gösterir. Variogramın monotonluğu ise, iki nokta arasındaki değişkenlik ilişkisinin uzaklıkla nasıl değiştiğini gösterir.

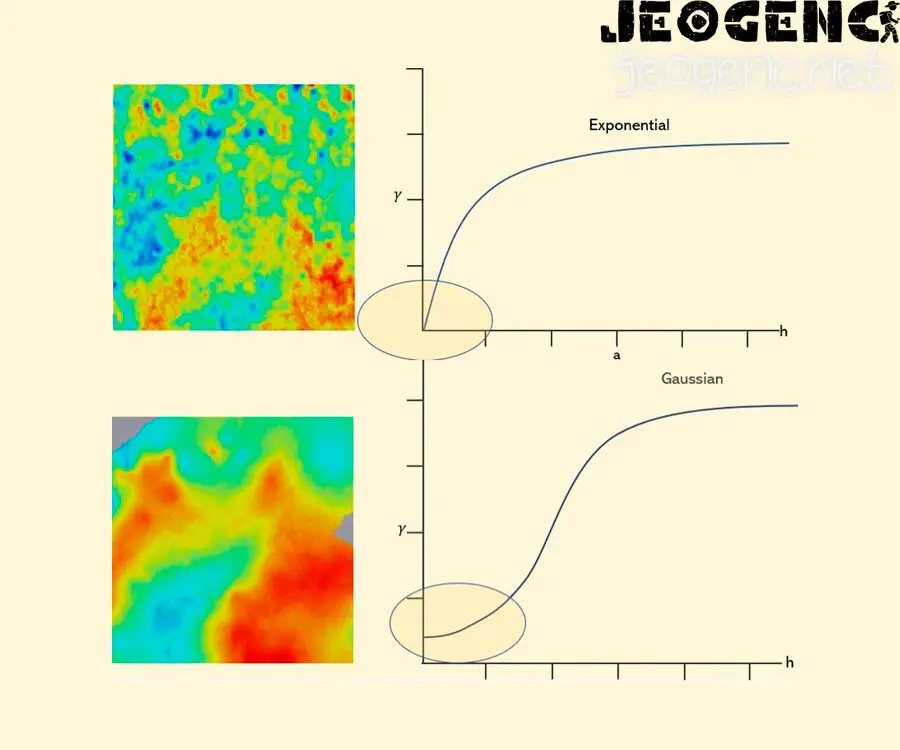
Variogram Temelleri: En kullanışlı jeoistatistik kavramlarından birine görsel bir giriş

Variogramın Simetrisi

İki nokta arasındaki değişkenlik ilişkisinin her iki yöne de aynı olduğunu gösterir. Örneğin, bir kayaçtaki minerallerin varyasyonunu inceleyen bir araştırmacı, bir noktanın 100 metre kuzeyindeki minerallerin varyasyonunu incelediğinde, aynı noktanın 100 metre güneyindeki minerallerin varyasyonunu incelediğinde aynı sonuçları elde eder.

Variogramın Monotonluğu

Variogramın monotonluğu, iki nokta arasındaki değişkenlik ilişkisinin uzaklıkla nasıl değiştiğini gösterir. Variogram, uzaklığın artmasıyla artar veya azalır.

Variogramın monotonluğu, değişkenin varyasyonunun nasıl değiştiğini anlamamıza yardımcı olur. Örneğin, bir değişkenin varyasyonunun uzaklıkla değişmediği durumlarda, variogram düz bir çizgi şeklinde olacaktır. Uzaklıkla azalan bir şekilde değiştiği durumlarda, variogram bir parabolik eğri şeklinde olacaktır. Variogramın uzaklıkla artan bir şekilde değiştiği durumlarda, variogram bir üssel eğri şeklinde olacaktır.

Variogramın Diğer Özellikleri

Diğer özellikleri şunlardır:

Variogramın sıfır noktası, iki nokta arasındaki uzaklığın sıfır olduğu noktadır.

Variogram tepe noktası, variogramın en yüksek olduğu noktadır.
Variogramın etki alanı, variogramın tepe noktasından sonra azalmaya başladığı uzaklıktır.

Variogramın bu özellikleri, variogramın şeklini ve değişkenin varyasyonunun uzaklıkla nasıl değiştiğini daha iyi anlamamıza yardımcı olur.

Variogram Modelleri

Variogramın şeklini tanımlamak için çeşitli modeller kullanılabilir. En yaygın variogram modelleri şunlardır:

Küresel model: Uzaklığın artmasıyla değişkenlik ilişkisinin sabit kaldığı modeldir.
Üssel model: Uzaklığın artmasıyla değişkenlik ilişkisinin artan bir şekilde azaldığı modeldir.
Gauss modeli: Bu modeli, uzaklığın artmasıyla değişkenlik ilişkisinin azalan bir şekilde azaldığı modeldir.

Külçe etkisi modeli: Uzaklığın artmasıyla değişkenlik ilişkisinin ani bir şekilde azaldığını gösteren modeldir.

Küresel Model

Bu model, uzaklığın artmasıyla değişkenlik ilişkisinin sabit kaldığı modeldir. Küresel modelin matematiksel formülasyonu şu şekildedir:

γ(h) = sill

Açıklamaları:

γ(h) = variogram değeri

sill = variogramın sill değeri

h = iki nokta arasındaki uzaklık

Küresel model, değişkenin varyasyonunun uzaklıkla değişmediği durumlarda kullanılır. Örneğin, bir kayaçtaki minerallerin varyasyonunu inceleyen bir araştırmacı, küresel model kullanabilir.

Üssel Model

Uzaklığın artmasıyla değişkenlik ilişkisinin artan bir şekilde azaldığı modeldir. Üssel modelin matematiksel formülasyonu şu şekildedir:

γ(h) = sill / (1 + h^2 / a^2)

Açıklamaları:

γ(h) = variogram değeri

sill = variogramın sill değeri

a = variogramın etki alanı

h = iki nokta arasındaki uzaklık

Üssel model, değişkenin varyasyonunun uzaklıkla azalan bir şekilde değiştiği durumlarda kullanılır. Örneğin, bir bölgedeki sıcaklığın varyasyonunu inceleyen bir araştırmacı, üssel model kullanabilir.

Gauss Modeli

Gauss modeli, uzaklığın artmasıyla değişkenlik ilişkisinin azalan bir şekilde azaldığı modeldir. Matematiksel formülasyonu şu şekildedir:

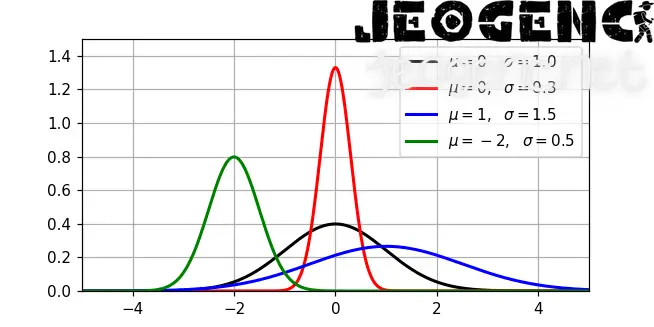
γ(h) = sill / (1 + (h / a)^2)

Açıklamaları:

γ(h) = variogram değeri

sill = variogramın sill değeri

a = variogramın etki alanı

h = iki nokta arasındaki uzaklık

Gauss modeli, değişkenin varyasyonunun uzaklıkla azalan bir şekilde değiştiği durumlarda kullanılır. Örneğin, bir toprağın geçirgenliğinin varyasyonunu inceleyen bir araştırmacı, Gauss model kullanabilir.

Külçe Etkisi Modeli

Bu külçe etkisi modeli, uzaklığın artmasıyla değişkenlik ilişkisinin ani bir şekilde azaldığını gösteren modeldir. Külçe etkisi modelin matematiksel formülasyonu şu şekildedir:

γ(h) = sill * (1 - exp(-h / a))

Açıklamaları:

γ(h) = variogram değeri

sill = variogramın sill değeri

a = variogramın etki alanı

h = iki nokta arasındaki uzaklık

Külçe etkisi modeli, değişkenin varyasyonunun uzaklıkla ani bir şekilde azaldığını gösteren durumlarda kullanılır. Örneğin, bir bölgedeki yağış miktarının varyasyonunu inceleyen bir araştırmacı, külçe etkisi model kullanabilir.

Variogram Modelinin Seçimi

Değişkenin varyasyonunun uzaklıkla nasıl değiştiğini anlamamıza yardımcı olur. Variogram modelinin seçimi yapılırken aşağıdaki faktörler dikkate alınmalıdır:

Variogramın şekli: Variogramın şekli, hangi variogram modelinin kullanılacağını belirlemede önemli bir faktördür.
Variogramın sill değeri: Variogramın sill değeri, değişkenin varyasyonunun büyüklüğünü gösterir.
Variogram etki alanı: Variogramın etki alanı, değişkenin varyasyonunun uzaklıkla nasıl değiştiğini gösterir.

Variogram modeli seçilirken, veri setinin büyüklüğü ve kalitesi de dikkate alınmalıdır. Veri seti yeterli büyüklükte ve kalitede değilse, variogram modelinin doğru bir şekilde belirlenmesi zor olabilir.

Variogram modeli, değişkenin varyasyonunun nasıl değiştiğini anlamamıza yardımcı olur. Örneğin, küresel model, değişkenin varyasyonunun uzaklıkla değişmediği durumlarda kullanılır. Üssel model, değişkenin varyasyonunun uzaklıkla azalan bir şekilde değiştiği durumlarda kullanılır. Gauss modeli, değişkenin varyasyonunun uzaklıkla azalan bir şekilde değiştiği durumlarda kullanılır. Külçe etkisi modeli, değişkenin varyasyonunun uzaklıkla ani bir şekilde azaldığını gösteren durumlarda kullanılır.

Variogramın Kullanım Alanları

Jeoloji, coğrafya, ekonomi, mühendislik ve diğer birçok alanda kullanılmaktadır. Variogramın bazı kullanım alanları şunlardır:

Jeolojide: Variogram, kayaçların ve toprakların varyasyonunu tanımlamak için kullanılır. Örneğin, variogram, bir kayaçtaki minerallerin varyasyonunu veya bir toprağın geçirgenliğinin varyasyonunu tanımlamak için kullanılabilir.
Coğrafyada: Variogram, iklim verilerinin varyasyonunu tanımlamak için kullanılır. Örneğin, variogram, bir bölgedeki sıcaklığın varyasyonunu veya bir bölgedeki yağış miktarının varyasyonunu tanımlamak için kullanılabilir.
Ekonomide: Variogram, ekonomik verilerin varyasyonunu tanımlamak için kullanılır. Örneğin, variogram, bir ülkenin gayri safi yurtiçi hasılasının varyasyonunu veya bir şirketin satışlarının varyasyonunu tanımlamak için kullanılabilir.

Mühendislikte: Variogram, mühendislik yapılarının varyasyonunu tanımlamak için kullanılır. Örneğin, variogram, bir köprüdeki gerilimin varyasyonunu veya bir binanın deformasyonunun varyasyonunu tanımlamak için kullanılabilir.

Variogram, aşağıdaki istatistiksel yöntemlerin uygulanmasında da kullanılır:

Kriging: Kriging, bir değişkenin değerlerinin bilinmeyen noktalarında tahmin edilmesinde kullanılan bir istatistiksel yöntemdir. Variogram, kriging yönteminin uygulanmasında kullanılır.
Geoestatistik: Geoestatistik, değişkenliğin uzayda nasıl değiştiğini inceleyen bir istatistiksel disiplindir. Variogram, geoestatistikte önemli bir araçtır.

Variogramın Hesaplanması

Variogram, iki nokta arasındaki uzaklık fonksiyonu olarak tanımlanır. Variogramın hesaplanması için aşağıdaki adımlar izlenir:

Veri seti, gözlem noktalarının konumlarına ve değerlerine göre düzenlenir.
İki nokta arasındaki uzaklıklar hesaplanır.
Her uzaklık için, iki nokta arasındaki değerler arasındaki varyasyon hesaplanır.

Variogram değerleri, her uzaklık için hesaplanan varyasyon değerlerinin bir fonksiyonu olarak çizilir.

Variogram Anizotropinin Hesaplanması ve Modellenmesi

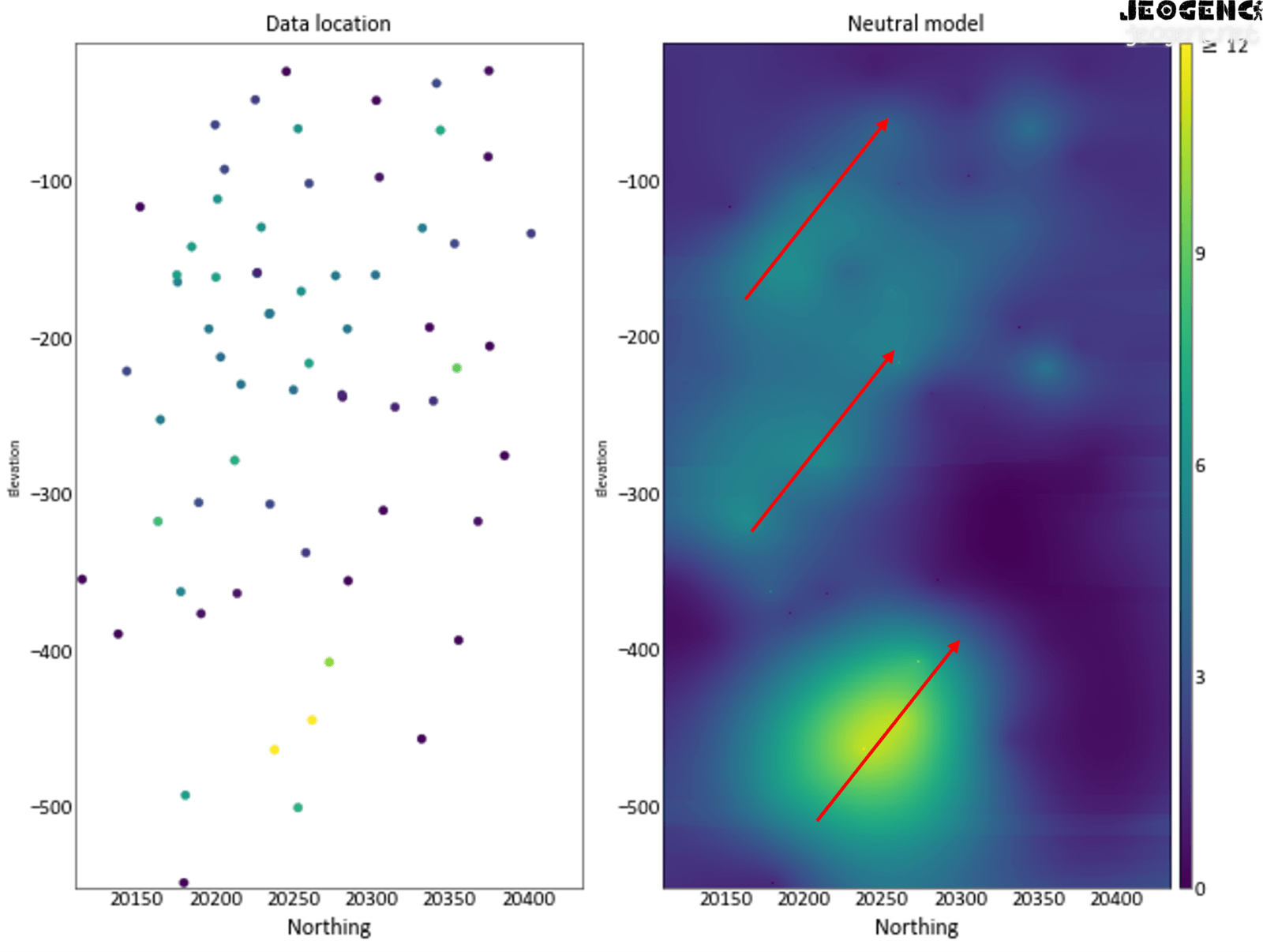
Variogramın hesaplanmasında kullanılan veri setinin büyüklüğü ve kalitesi, variogramın doğruluğunu etkiler. Veri seti yeterli büyüklükte ve kalitede değilse, variogramın doğru bir şekilde belirlenmesi zor olabilir.

Variogramın Sınırlamaları

Değişkenin varyasyonunun uzaklıkla nasıl değiştiğini anlamamıza yardımcı olan önemli bir araçtır. Ancak, variogramın bazı sınırlamaları da vardır:

Variogram, değişkenin varyasyonunu tam olarak tanımlayamaz. Variogram, sadece değişkenin varyasyonunun uzaklıkla nasıl değiştiğini tahmin eder.
Variogramın, veri setinin büyüklüğüne ve kalitesine göre hassastır. Veri seti yeterli büyüklükte ve kalitede değilse, variogramın doğruluğunu etkileyebilir.

Variogram, değişkenin varyasyonunun uzaklıkla nasıl değiştiğini anlamamıza yardımcı olan önemli bir araçtır. Jeoloji, coğrafya, ekonomi, mühendislik ve diğer birçok alanda kullanılmaktadır. Variogram, kriging gibi istatistiksel yöntemlerin uygulanmasında da kullanılır.